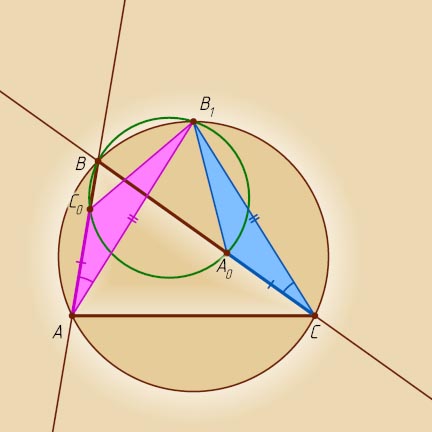
6436. На сторонах AB
и BC
неравнобедренного треугольника ABC
выбраны точки C_{0}
и A_{0}
соответственно, точка B_{1}
— середина дуги ABC
описанной окружности треугольника ABC
. Докажите, что равенство AC_{0}=CA_{0}
выполняется тогда и только тогда, когда точки A_{0}
, C_{0}
, B_{1}
и B
лежат на одной окружности.
Решение. Рассмотрим случай, изображённый на рисунке.
Необходимость. Пусть AC_{0}=CA_{0}
, а окружность, проходящая через точки B
, A_{0}
и C_{0}
, пересекает описанную окружность треугольника ABC
в точке B'
, отличной от B
. По теореме о вписанных углах, опирающихся на одну и ту же дугу,
\angle C_{0}AB'=\angle BAB'=\angle BCB'=\angle A_{0}CB',
\angle BC_{0}B'=\angle BA_{0}B'.
Тогда
\angle AC_{0}B'=180^{\circ}-\angle BC_{0}B'=180^{\circ}-\angle BA_{0}B'=\angle CA_{0}B',
значит, треугольники AC_{0}B'
и CA_{0}B'
равны по стороне и двум прилежащим к ней углам, поэтому AB'=CB'
. Следовательно, точка B'
совпадает с серединой B_{1}
дуги ABC
описанной окружности треугольника ABC
. Что и требовалось доказать.
Достаточность. Пусть точки A_{0}
, C_{0}
, B_{1}
и B
лежат на одной окружности. Тогда AB_{1}=CB_{1}
. По теореме о вписанных углах
\angle C_{0}AB_{1}=\angle BAB_{1}=\angle BCB_{1}=\angle A_{0}CB_{1},
\angle AB_{1}C=\angle ABC=\angle C_{0}BA_{0}=\angle C_{0}B_{1}A_{0}.
Значит,
\angle C_{0}B_{1}A=\angle C_{0}B_{1}A_{0}-\angle AB_{1}A_{0}=\angle ABC-\angle AB_{1}A_{0}=\angle CB_{1}A_{0},
поэтому треугольники AC_{0}B_{1}
и CA_{0}B_{1}
равны по стороне и двум прилежащим к ней углам. Следовательно, AC_{0}=CA_{0}
. Что и требовалось доказать.
Аналогично для остальных случаев.
Примечание. 1. Утверждение остаётся справедливым и для случаев, когда точки A_{0}
и C_{0}
расположены на прямых (а не только на отрезках) AB
и BC
. Тогда, если C_{0}
не лежит на луче AB
и (или) A_{0}
не лежит на луче CB
, то длины отрезков AC_{0}
и (или) CA_{0}
будем считать отрицательными.
2. См. статью А.Полянского «Воробьями по пушкам!», Квант, 2012, N2, с.49-50.
Источник: Журнал «Квант». — 2012, № 2, с. 49-50
