6455. В остроугольном треугольнике ABC
через центр O
описанной окружности и вершины B
и C
проведена окружность S
. Пусть OK
— диаметр окружности S
; D
и E
— соответственно точки её пересечения с прямыми AB
и AC
. Докажите, что ADKE
— параллелограмм.
Указание. Докажите, что \angle AEK=180^{\circ}-\angle A
.
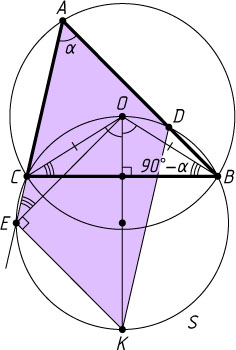
Решение. Без ограничения общности рассмотрим случай, когда точка D
лежит на стороне AB
, а точка E
— на продолжении стороны AC
за точку C
(см.рис.).
Обозначим \angle BAC=\alpha
. Тогда
\angle BOC=2\alpha,~\angle OBC=\angle OCB=90^{\circ}-\alpha.
Поскольку точка E
лежит на окружности с диаметром OK
, то \angle OEK=90^{\circ}
, а так как вписанные в окружность S
углы OEC
и OBC
опираются на одну и ту же дугу, то
\angle OEC=\angle OBC=90^{\circ}-\alpha.
Поэтому
\angle AEK=\angle OEK+\angle OEC=90^{\circ}+90^{\circ}-\alpha=180^{\circ}-\alpha.
Значит, AD\parallel KE
. Аналогично AE\parallel DK
. Следовательно, ADKE
— параллелограмм.
Автор: Сонкин М. Г.
Источник: Всероссийская олимпиада школьников. — 1997-98, XXIV, окружной этап, 10 класс
Источник: Журнал «Квант». — 1998, № 5, с. 51
Источник: Агаханов Н. Х. и др. Всероссийские математические олимпиады школьников. 1993—2006. — М.: МЦНМО, 2007. — № 154, с. 25
