6459. Две окружности пересекаются в точках P
и Q
. Прямая пересекает эти окружности последовательно в точках A
, B
, C
и D
, как показано на рисунке. Докажите, что \angle APB=\angle CQD
.
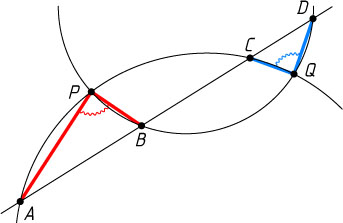
Указание. Проведите общую хорду данных окружностей и воспользуйтесь теоремой о вписанных углах.
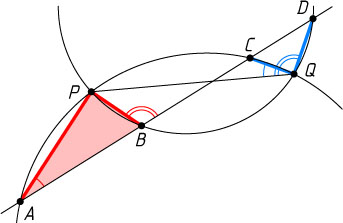
Решение. По теореме о вписанных углах
\angle PAC=\angle PQC,~\angle PBD=\angle PQD.
Поскольку PBD
— внешний угол треугольника ABP
, то
\angle PBD=\angle PAB+\angle APB.
Следовательно,
\angle APB=\angle PBD-\angle PAB=\angle PBD-\angle PAC=\angle PQD-\angle PQC=\angle CQD,
что и требовалось доказать.
Автор: Кожевников П. А.
Источник: Всероссийская олимпиада школьников. — 1997-98, XXIV, окружной этап, 9 класс
Источник: Журнал «Квант». — 1998, № 5, с. 50
Источник: Журнал «Crux Mathematicorum». — 2006, № 5, с. 280
Источник: Исландские математические олимпиады. — 2000-2001
Источник: Московская математическая регата. — 2012-2013, 9 класс
Источник: Агаханов Н. Х. и др. Всероссийские математические олимпиады школьников. 1993—2006. — М.: МЦНМО, 2007. — № 146, с. 24

