6463. Прямая отсекает от правильного десятиугольника ABCDEFGHIJ
со стороной 1 треугольник PAQ
, в котором PA+AQ=1
. Найдите сумму углов, под которыми виден отрезок PQ
из вершин B
, C
, D
, E
, F
, G
, H
, I
, J
.
Ответ. \frac{4\pi}{5}
.
Указание. Правильный десятиугольник переходит в себя при повороте вокруг его центра на любой угол, кратный \frac{\pi}{5}
.
Решение. Для определённости будем считать, что точка P
лежит на стороне JA
, а точка Q
— на стороне AB
. Из условия задачи следует, что PA=QB
. На сторонах BC
, CD
, \dots
, IJ
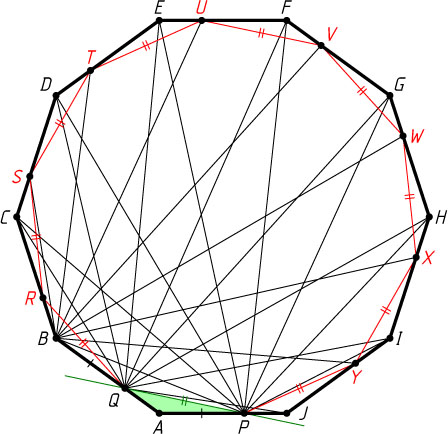
десятиугольника рассмотрим такие точки R
, S
, \dots
, Y
(R\in BC
, S\in CD
, \dots
, Y\in IJ
), что QB=RC=SD=\dots=YJ
. Отсюда и из равенства всех внутренних углов десятиугольника следует, что PQ=QR=RS=ST=\dots=YP
.
Поскольку правильный десятиугольник переходит в себя при повороте вокруг его центра на любой угол, кратный \frac{2\pi}{10}
, и при этом множество точек P
, Q
, R
, S
, \dots
, Y
также переходит в себя, то
\triangle QCP=\triangle PBY,~\triangle QDP=\triangle YBX,~\dots,~\triangle QJP=\triangle SBR.
Значит, искомая сумма углов равна внутреннему углу десятиугольника при вершине B
, т. е. \pi-\frac{2\pi}{10}=\frac{4\pi}{5}
.
Автор: Произволов В. В.
Источник: Турнир городов. — 1994-1995, XVI, весенний тур, младшие классы, основной вариант
