6470. В треугольнике ABC
на сторонах AC
и BC
взяты соответственно точки X
и Y
, причём \angle ABX=\angle YAC
, \angle AYB=\angle BXC
, XC=YB
. Найдите углы треугольника ABC
.
Ответ. 60^{\circ}
, 60^{\circ}
, 60^{\circ}
.
Решение. Лемма. Если стороны K_{1}L_{1}
, K_{1}M_{1}
и угол K_{1}L_{1}M_{1}
треугольника K_{1}L_{1}M_{1}
соответственно равны сторонам KL
, KM
и углу KLM
треугольника KLM
, то либо \angle K_{1}M_{1}L_{1}=\angle KML
и тогда треугольник K_{1}L_{1}M_{1}
равен треугольнику KLM
, либо \angle K_{1}M_{1}L_{1}=180^{\circ}-\angle KML
.
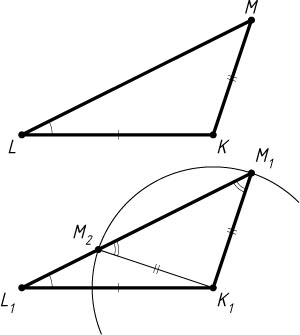
Доказательство. Пусть дан треугольник KLM
(рис. 1). Построим треугольник K_{1}L_{1}M_{1}
по данным сторонам K_{1}L_{1}=KL
, K_{1}M_{1}=K_{1}L_{1}
и углу K_{1}L_{1}M_{1}
, равному углу KLM
. Для этого от начала произвольного луча отложим отрезок L_{1}K_{1}=LK
, затем в одну из плоскостей, на которые разбивает плоскость прямая L_{1}K_{1}
, отложим луч L_{1}P
, образующий с лучом L_{1}K_{1}
угол, равный данному углу KLM
. С центром в точке K_{1}
построим окружность радиусом, равным KM
. Если эта окружность не пересекается с построенным лучом, то задача не имеет решений; если окружность имеет с лучом единственную общую точку, то задача имеет одно решение; если окружность пересекает луч в двух точках M_{1}
и M_{2}
(точка M_{2}
лежит между L_{1}
и M_{1}
), то треугольник M_{1}K_{1}M_{2}
— равнобедренный, поэтому либо
\angle K_{1}M_{2}L_{1}=180^{\circ}-\angle K_{1}M_{2}M_{1}=180^{\circ}-\angle K_{1}M_{1}M_{2}=180^{\circ}-\angle K_{1}M_{1}L_{1}=180^{\circ}-\angle KLM,
\angle K_{1}M_{1}L_{1}=\angle KML,
либо наоборот,
\angle K_{1}M_{2}L_{1}=\angle KLM,~\angle K_{1}M_{1}L_{1}=180^{\circ}-\angle KML.
Лемма доказана.
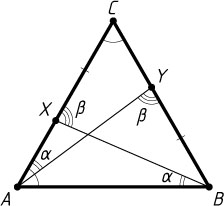
Рассмотрим теперь нашу задачу. Обозначим \angle ABX=\angle YAC=\alpha
, \angle AYB=\angle BXC=\beta
(рис. 2). Поскольку AYB
и BXC
— внешние углы треугольников AYC
и AXB
, то
\angle ACB=\angle ACY=\angle AYB-\angle YAC=\beta-\alpha=\angle BXC-\angle ABX=\angle BAX=\angle BAC.
Значит, треугольник ABC
— равнобедренный, AB=BC
.
Рассмотрим треугольники XBC
и YAB
. Известно, что BC=AB
, CX=YB
и \angle BXC=\angle AYB
. Из доказанной леммы следует, что либо треугольники XBC
и YAB
равны, либо \angle XBC+\angle YAB=180^{\circ}
. Второй вариант невозможен, так как в этом случае сумма углов треугольника AYB
была бы больше 180^{\circ}
.
Таким образом, из равенства треугольников и XBC
и YAB
следует равенство углов ACB
и ABC
, значит, треугольник ABC
— равносторонний.
Автор: Казицина (Караваева) Т. В.
Источник: Московская математическая олимпиада. — 2003, LXVI, 8 класс
Источник: Журнал «Квант». — 2003, № 4, с. 53
Источник: Фёдоров Р. М. и др. Московские математические олимпиады. 1993—2005 / Под ред. В. М. Тихомирова. — М.: МЦНМО, 2006. — № 4, с. 56

