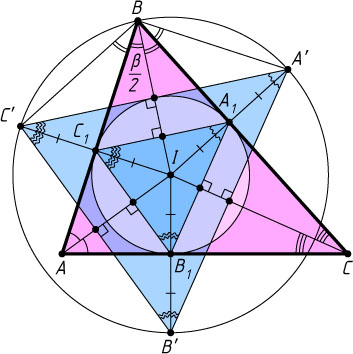
6474. Пусть I
— точка пересечения биссектрис треугольника ABC
. Обозначим через A'
, B'
, C'
точки, симметричные точке I
относительно сторон треугольника ABC
. Докажите, что если окружность, описанная около треугольника A'B'C'
, проходит через вершину B
, то \angle ABC=60^{\circ}
.
Решение. Точка I
— центр вписанной окружности треугольника ABC
. Обозначим точки касания этой окружности со сторонами AB
, BC
и AC
через A_{1}
, B_{1}
и C_{1}
соответственно. Тогда точки A_{1}
, B_{1}
и C_{1}
— середины отрезков соответственно IA'
, IB'
и IC'
. По теореме о средней линии треугольника A_{1}B_{1}\parallel A'B'
, B_{1}C_{1}\parallel B'C'
и A_{1}C_{1}\parallel A'C'
. Значит, углы треугольника A_{1}B_{1}C_{1}
соответственно равны углам треугольника A'B'C'
.
Обозначим \angle ABC=\beta
. Поскольку B_{1}C_{1}\perp AI
и B_{1}A_{1}\perp CI
, а AI
и CI
— биссектрисы углов BAC
и BCA
треугольника ABC
, то
\angle A'B'C'=\angle A_{1}B_{1}C_{1}=180^{\circ}-\angle AIC=180^{\circ}-\left(90^{\circ}+\frac{\beta}{2}\right)=90^{\circ}-\frac{\beta}{2},
а так как A'B'C'
и A'BC'
— противоположные углы вписанного четырёхугольника A'B'C'B
, то
\angle A'BC'=180^{\circ}-\angle A'B'C'=180^{\circ}-\left(90^{\circ}-\frac{\beta}{2}\right)=90^{\circ}+\frac{\beta}{2}.
С другой стороны, поскольку точки A'
и C'
симметричны точке I
относительно прямых соответственно BC
и AB
, то
\angle A'BC'=\angle C'BI+\angle A'BI=2\angle ABI+2\angle CBI=2(\angle ABI+\angle CBI)=2\angle ABC=2\beta.
Из уравнения 90^{\circ}+\frac{\beta}{2}=2\beta
находим, что \beta=60^{\circ}
.
Автор: Емельянов Л. А.
Источник: Всероссийская олимпиада школьников. — 2002-03, XXIX, окружной этап, 9 класс
Источник: Журнал «Квант». — 2003, № 5, с. 44
Источник: Агаханов Н. Х. и др. Всероссийские математические олимпиады школьников. 1993—2006. — М.: МЦНМО, 2007. — № 309, с. 43
