6475. Окружности S_{1}
и S_{2}
с центрами O_{1}
и O_{2}
соответственно пересекаются в точках A
и B
. Касательные к S_{1}
и S_{2}
в точке A
пересекают отрезки BO_{2}
и BO_{1}
в точках K
и L
соответственно. Докажите, что KL\parallel O_{1}O_{2}
.
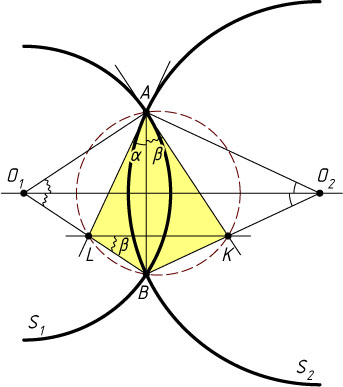
Решение. Обозначим \angle BAL=\alpha
, \angle BAK=\beta
. Из теоремы об угле между касательной и хордой следует, что
\angle AO_{2}B=2\angle BAL=2\alpha,~\angle AO_{1}B=2\angle BAK=2\beta,
поэтому
\angle BO_{2}O_{1}=\frac{1}{2}\angle AO_{2}B=\alpha,~\angle BO_{1}O_{2}=\frac{1}{2}\angle AO_{1}B=\beta.
Из треугольника O_{1}BO_{2}
находим, что
\angle O_{1}BO_{2}=180^{\circ}-\alpha-\beta=180^{\circ}-\angle LAK.
Значит, четырёхугольник AKBL
— вписанный. Тогда
\angle KLB=\angle KAB=\beta=\angle O_{2}O_{1}B.
Следовательно, KL\parallel O_{1}O_{2}
.
Автор: Емельянов Л. А.
Источник: Всероссийская олимпиада школьников. — 2002-03, XXIX, заключительный этап, 9 класс
Источник: Журнал «Квант». — 2003, № 5, с. 45
Источник: Агаханов Н. Х. и др. Всероссийские математические олимпиады школьников. 1993—2006. — М.: МЦНМО, 2007. — № 666, с. 86
Источник: Журнал «Crux Mathematicorum». — 2008, № 6, задача M313, с. 329
