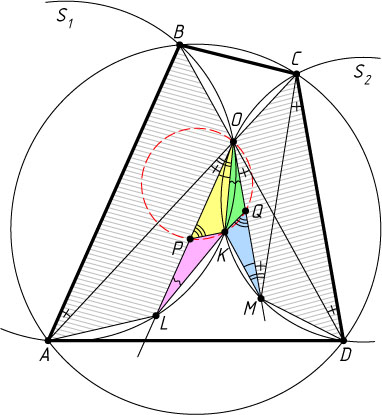
6476. Диагонали вписанного четырёхугольника ABCD
пересекаются в точке O
. Пусть S_{1}
и S_{2}
— окружности, описанные около треугольников ABO
и CDO
соответственно, O
и K
— точки пересечения окружностей S_{1}
и S_{2}
. Прямые, проходящие через точку O
параллельно прямым AB
и CD
, вторично пересекают S_{1}
и S_{2}
в точках L
и M
соответственно. На отрезках OL
и OM
выбраны соответственно точки P
и Q
, причём OP:PL=MQ:QO
. Докажите, что точки O
, K
, P
, Q
лежат на одной окружности.
Решение. Не умаляя общности, можно считать, что \angle ABO\geqslant\angle BAO
, тогда ABOL
и DCOM
— равнобедренные трапеции. Из теоремы о вписанных углах следует, что
\angle LOA=\angle OAB=\angle ODC=\angle DOM=\angle DCM=\angle CMO,
а так как
\angle KMC=180^{\circ}-\angle KOC=\angle KOA,
то \angle KMO=\angle KOL
. Аналогично \angle KLO=\angle KOM
. Значит, треугольники KOM
и KLO
подобны по двум углам. Но тогда подобны и треугольники KOP
и KMQ
(\frac{OP}{PL}=\frac{MQ}{QO}
по условию задачи). Поэтому
\angle KPO=\angle KQM=180^{\circ}-\angle KQO.
Следовательно, четырёхугольник KPOQ
— вписанный.
Автор: Берлов С. Л.
Источник: Всероссийская олимпиада школьников. — 2002-03, XXIX, заключительный этап, 10 класс
Источник: Журнал «Квант». — 2003, № 5, с. 46
Источник: Агаханов Н. Х. и др. Всероссийские математические олимпиады школьников. 1993—2006. — М.: МЦНМО, 2007. — № 674, с. 87
