6477. В треугольнике ABC
через O
, I
обозначены центры описанной и вписанной окружностей соответственно. Вневписанная окружность \omega_{a}
касается продолжений сторон AB
и AC
в точках K
и M
соответственно, а стороны BC
— в точке N
. Известно, что середина P
отрезка KM
лежит на описанной окружности треугольника ABC
. Докажите, что точки O
, N
и I
лежат на одной прямой.
Решение. Лемма. (Теорема Мансиона.) Отрезок, соединяющий центры вписанной и вневписанной окружностей треугольника, делится описанной окружностью пополам.
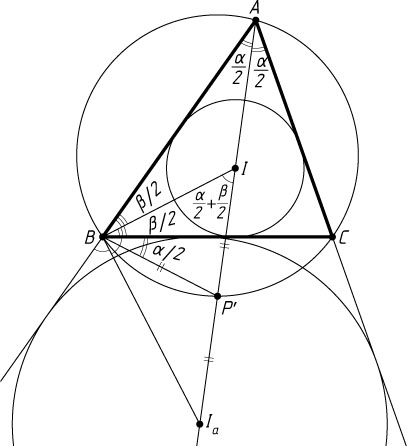
Доказательство. Пусть I_{a}
— центр вневписанной окружности \omega_{a}
треугольника ABC
, касающейся стороны BC
(рис. 1), P'
— точка пересечения отрезка II_{a}
с описанной окружностью треугольника ABC
. Поскольку центр окружности, вписанной в угол, лежит на биссектрисе этого угла, то точки A
, I
и I_{a}
лежат на одной прямой. Обозначим углы треугольника ABC
через \alpha
, \beta
, \gamma
соответственно. Тогда
\angle BIP'=\angle BAI+\angle ABI=\frac{\alpha}{2}+\frac{\beta}{2},
\angle P'BI=\angle P'BC+\angle CBI=\angle P'AC+\angle CBI=\frac{\alpha}{2}+\frac{\beta}{2}.
Следовательно, треугольник BIP'
— равнобедренный, P'I=P'B
. Аналогично P'I=P'C
.
Поскольку BI
и BI_{a}
— биссектрисы смежных углов, то \angle IBI_{a}=90^{\circ}
. Точка P'
равноудалена от концов отрезка BI
, поэтому она лежит на серединном перпендикуляре к катету BI
прямоугольного треугольника IBI_{a}
, а значит, совпадает с серединой гипотенузы II_{a}
. Лемма доказана.
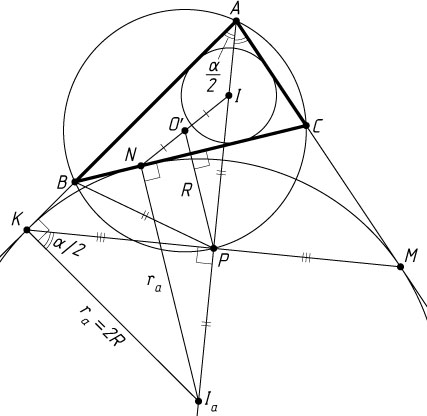
Рассмотрим теперь нашу задачу (рис. 2). Поскольку AK=AM
(как отрезки касательных, проведённых из точки A
к окружности \omega_{a}
), то треугольник AKM
— равнобедренный, поэтому середина P
его основания KM
лежит на биссектрисе угла при вершине A
, а значит, на отрезке II_{a}
. С другой стороны, точка P
— это точка пересечения отрезка, соединяющего центры вписанной и вневписанной окружностей треугольника, с описанной окружностью этого треугольника, значит, по доказанному, P
— середина II_{a}
. Следовательно, BP=IP=I_{a}P
.
Пусть R
— радиус описанной окружности треугольника ABC
, r_{a}
— радиус окружности \omega_{a}
. Из прямоугольного треугольника KPI_{a}
находим, что
PI_{a}=KI_{a}\sin\angle PKI_{a}=r_{a}\sin\frac{\alpha}{2}.
По теореме синусов находим, что
PB=2R\sin\frac{\alpha}{2},
а так как PI_{a}=PB
, то r_{a}=2R
.
Пусть O'
— середина отрезка NI
. Тогда по теореме о средней линии треугольника O'P\parallel NI_{a}
, а так как I_{a}N\perp BC
, то O'P\perp BC
и
O'P=\frac{1}{2}I_{a}N=\frac{r_{a}}{2}=R.
В то же время, OP\perp BC
и OP=R
, поэтому O
и O'
совпадают. Следовательно, точки O
, N
и I
лежат на одной прямой.
Автор: Кожевников П. А.
Источник: Всероссийская олимпиада школьников. — 2002-03, XXIX, заключительный этап, 10 класс
Источник: Журнал «Квант». — 2003, № 5, с. 46
Источник: Агаханов Н. Х. и др. Всероссийские математические олимпиады школьников. 1993—2006. — М.: МЦНМО, 2007. — № 679, с. 88

