6491. На большей стороне AC
треугольника ABC
взята точка N
так, что серединные перпендикуляры к отрезкам AN
и NC
пересекают стороны AB
и BC
в точках K
и M
соответственно. Докажите, что центр O
описанной около треугольника ABC
окружности лежит на окружности, описанной около треугольника KBM
.
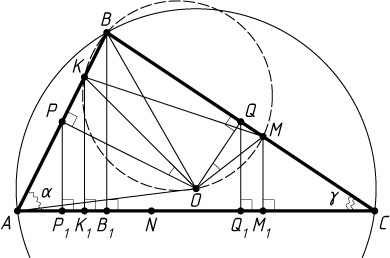
Решение. Пусть P
и Q
— середины сторон AB
и BC
соответственно, P_{1}
, K_{1}
, Q_{1}
, M_{1}
, B_{1}
— проекции точек P
, K
, Q
, M
, B
на сторону AC
. Поскольку P_{1}
— середина AB_{1}
, а Q_{1}
— середина CB_{1}
, то
P_{1}Q_{1}=\frac{1}{2}AB_{1}+\frac{1}{2}CB_{1}=\frac{1}{2}(AB_{1}+CB_{1})=\frac{1}{2}AC.
Поскольку K_{1}
— середина AN
, а M_{1}
— середина CN
, то
K_{1}M_{1}=\frac{1}{2}AN+\frac{1}{2}CN=\frac{1}{2}(AN+CN)=\frac{1}{2}AC.
Поэтому P_{1}Q_{1}=K_{1}M_{1}
. Поэтому, если K
точка ближе к вершине B
, чем точка P
, то точка Q
ближе к B
, чем точка M
.
Из условия задачи следует, что OP\perp AB
и OQ\perp BC
, поэтому
\angle POQ=180^{\circ}-\angle ABC,
Таким образом, утверждение задачи равносильно равенству \angle KOM=\angle POQ
(тогда сумма противоположных углов четырёхугольника BKOM
равна 180^{\circ}
, а значит, точки B
, K
, O
и M
лежат на одной окружности).
С учётом установленного расположения точек, достаточно доказать, что \angle POK=\angle QOM
, что равносильно подобию прямоугольных треугольников OPK
и OQM
.
Пусть \angle BAC=\alpha
, \angle ACB=\gamma
. Поскольку P_{1}K_{1}
и Q_{1}M_{1}
— проекции отрезков PK
и QM
на прямую AC
, то
PK=\frac{P_{1}K_{1}}{\cos\alpha},~QM=\frac{Q_{1}M_{1}}{\cos\gamma},
а так как P_{1}Q_{1}=K_{1}M_{1}
, то P_{1}K_{1}=Q_{1}M_{1}
, поэтому
\frac{PK}{QM}=\frac{\frac{P_{1}K_{1}}{\cos\alpha}}{\frac{Q_{1}M_{1}}{\cos\gamma}}=\frac{\cos\gamma}{\cos\alpha}.
С другой стороны, AOB
— центральный угол описанной окружности треугольника ABC
, а ACB
— угол, вписанный в эту окружность, поэтому \angle AOB=2\angle ACB=2\gamma
, а \angle BOP=\frac{1}{2}\angle AOB=\gamma
. Если R
— радиус описанной окружности треугольника ABC
, то из прямоугольного треугольника BPO
находим, что OP=OB\cos\gamma=R\cos\gamma
. Аналогично находим, что OQ=R\cos\alpha
. Поэтому
\frac{OP}{OQ}=\frac{R\cos\gamma}{R\cos\alpha}=\frac{\cos\gamma}{\cos\alpha}=\frac{PK}{QM}.
Следовательно, треугольники OPK
и OQM
подобны. Отсюда следует утверждение задачи.
Автор: Берлов С. Л.
Источник: Всероссийская олимпиада школьников. — 2000-01, XXVII, заключительный этап, 9 класс
Источник: Журнал «Квант». — 2001, № 5, с. 50
Источник: Агаханов Н. Х. и др. Всероссийские математические олимпиады школьников. 1993—2006. — М.: МЦНМО, 2007. — № 623, с. 81
