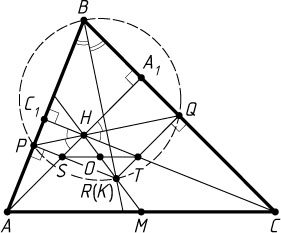
6497. В остроугольном неравнобедренном треугольнике ABC
биссектриса угла между высотами AA_{1}
и CC_{1}
пересекает стороны AB
и BC
в точках P
и Q
соответственно. Биссектриса угла B
пересекает отрезок, соединяющий ортоцентр треугольника ABC
с серединой стороны AC
, в точке R
. Докажите, что точки P
, B
, Q
и R
лежат на одной окружности.
Решение. Пусть H
— точка пересечения высот (ортоцентр) треугольника ABC
, а M
— середина стороны AC
. Пусть перпендикуляр, восставленный к стороне AB
в точке P
, пересекает высоту AA_{1}
в точке S
, а перпендикуляр, восставленный к стороне BC
в точке Q
, пересекает высоту CC_{1}
в точке T
. Если K
— точка пересечения этих перпендикуляров, то четырёхугольник BPKQ
— вписанный (из точек P
и Q
отрезок BK
виден под прямым углом). Утверждение задачи равносильно тому, что точка K
совпадает с R
.
Поскольку
\angle BPQ=\angle C_{1}PH=90^{\circ}-\angle C_{1}HP=90^{\circ}-\angle CHQ=90^{\circ}-\angle A_{1}HQ=\angle A_{1}QH=\angle BQP,
то треугольник PQB
— равнобедренный, BP=BQ
. Из равенства прямоугольных треугольников BPK
и BQK
следует, что точка K
лежит на биссектрисе угла B
. Осталось доказать, что точка K
лежит на прямой HM
.
Действительно, треугольник PHC_{1}
подобен треугольнику QHA_{1}
, треугольник AHC_{1}
— треугольнику CHA_{1}
, а треугольник PHS
— треугольнику THQ
, поэтому
\frac{PH}{HQ}=\frac{C_{1}H}{HA_{1}},~\frac{C_{1}H}{HA_{1}}=\frac{AH}{HC},~\frac{PH}{HQ}=\frac{HS}{HT}.
Следовательно,
\frac{HS}{HT}=\frac{PH}{HQ}=\frac{C_{1}H}{HA_{1}}=\frac{AH}{HC}.
Значит, ST\parallel AC
. Поэтому медиана HM
треугольника AHC
проходит через середину O
отрезка ST
, а так как четырёхугольник HTKS
— параллелограмм, то O
— точка пересечения его диагоналей, поэтому точка K
лежит на прямой HO
, а значит, на прямой HM
.
Следовательно, K
— точка пересечения прямой MH
с биссектрисой угла B
, а значит, совпадает с точкой R
, что и требовалось доказать.
Автор: Берлов С. Л.
Источник: Всероссийская олимпиада школьников. — 1999-2000, XXVI, заключительный этап, 10 класс
Источник: Журнал «Квант». — 2000, № 5, с. 51
Источник: Агаханов Н. Х. и др. Всероссийские математические олимпиады школьников. 1993—2006. — М.: МЦНМО, 2007. — № 603, с. 78
