6504. Треугольник ABC
вписан в окружность S
. Пусть A_{0}
— середина дуги BC
окружности S
, не содержащей точку A
, C_{0}
— середина дуги окружности S
, не содержащей точку C
. Окружность S_{1}
с центром A_{0}
касается BC
, окружность S_{2}
с центром C_{0}
касается AB
. Докажите, что центр I
вписанной в треугольник ABC
окружности лежит на одной из общих внешних касательных к окружностям S_{1}
и S_{2}
.
Решение. Из точки I
проведём касательную IK
к окружности S_{1}
так, чтобы она пересекала меньшую дугу A_{0}C
. Аналогичным образом проведём касательную IL
к окружности S_{2}
.
Биссектриса AI
угла BAC
делит дугу BC
пополам, поэтому точки A
, I
и A_{0}
лежат на одной прямой. Аналогично докажем, что точки C
, I
и C_{0}
лежат на одной прямой. Положим \angle BAC=2\alpha
, \angle ACB=2\gamma
. По теореме о внешнем угле треугольника
\angle A_{0}IC=\angle IAC+\angle ICA=\alpha+\gamma.
С другой стороны,
\angle A_{0}CI=\angle A_{0}CB+\angle ICB=\angle IAB+\angle ICB=\alpha+\gamma=\angle A_{0}IC.
Значит, треугольник A_{0}CI
— равнобедренный, A_{0}I=A_{0}C
.
Пусть D
— середина стороны BC
. Тогда окружность S_{1}
касается BC
в точке D
.
Прямоугольные треугольники A_{0}KI
и A_{0}DC
равны по катету (A_{0}K=A_{0}D
как радиусы одной окружности) и гипотенузе (A_{0}I=A_{0}C
по доказанному). Поэтому
\angle A_{0}IK=\angle A_{0}CD=\alpha=\angle A_{0}AC.
Следовательно, IK\parallel AC
.
Аналогично докажем, что IL\parallel AC
. Следовательно, точки L
, I
, K
лежат на одной прямой, параллельной AC
.
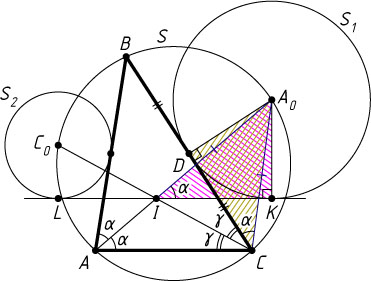
Автор: Сонкин М. Г.
Источник: Всероссийская олимпиада школьников. — 1998-99, XXV, заключительный этап, 9 класс
Источник: Журнал «Квант». — 1999, № 5, с. 50
Источник: Агаханов Н. Х. и др. Всероссийские математические олимпиады школьников. 1993—2006. — М.: МЦНМО, 2007. — № 571, с. 74
