6508. Окружность, вписанная в четырёхугольник ABCD
, касается его сторон DA
, AB
, BC
и CD
в точках K
, L
, M
и N
соответственно. Пусть S_{1}
, S_{2}
, S_{3}
и S_{4}
— окружности, вписанные в треугольники AKL
, BLM
, CMN
и DNK
соответственно. К окружностям S_{1}
и S_{2}
, S_{2}
и S_{3}
, S_{3}
и S_{4}
, S_{4}
и S_{1}
проведены общие внешние касательные, отличные от сторон четырёхугольника ABCD
. Докажите, что четырёхугольник, образованный этими четырьмя касательными, — ромб.
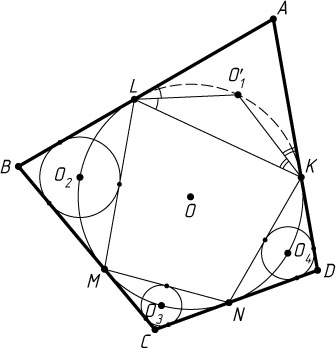
Решение. 1) Докажем сначала, что центры O_{1}
, O_{2}
, O_{3}
и O_{4}
окружностей S_{1}
, S_{2}
, S_{3}
и S_{4}
, вписанных в треугольники AKL
, BLM
, CMN
и DNK
соответственно, совпадают с серединами соответствующих дуг окружности S
, вписанной в четырёхугольник ABCD
(рис. 1).
Действительно, пусть O_{1}'
— середина меньшей дуги KL
окружности S_{1}
. Тогда из теоремы об угле между касательной и хордой следует, что
\angle AKO_{1}'=\angle KLO_{1}'=\angle LKO_{1}'.
Аналогично, \angle ALO_{1}'=\angle KLO_{1}'
, значит, O_{1}'
— точка пересечения биссектрис треугольника AKL
. Следовательно, точки O_{1}'
и O_{1}
совпадают.
Аналогично докажем, что O_{2}
, O_{3}
и O_{4}
— середины меньших дуг соответственно LM
, MN
И KN
окружности S
.
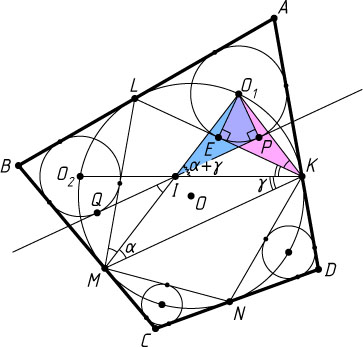
2) Докажем, что центр I
окружности, вписанной в треугольник KLM
, лежит на общей касательной окружностей S_{1}
и S_{2}
, не совпадающей с прямой AB
(рис. 2).
Из точки I
проведём касательную IP
к окружности S_{1}
так, чтобы она пересекала меньшую дугу O_{1}K
окружности S
. Аналогичным образом проведём касательную IQ
к окружности S_{2}
.
Биссектриса MI
угла KML
делит дугу KL
пополам, поэтому точки M
, I
и O_{1}
лежат на одной прямой. Аналогично докажем, что точки K
, I
и O_{2}
лежат на одной прямой.
Положим \angle KML=2\alpha
, \angle MKL=2\gamma
. По теореме о внешнем угле треугольника
\angle O_{1}IK=\angle IMK+\angle IKM=\alpha+\gamma.
С другой стороны,
\angle O_{1}KI=\angle O_{1}KL+\angle IKL=\alpha+\gamma=\angle O_{1}IK.
Значит, треугольник O_{1}KI
— равнобедренный, O_{1}I=O_{1}K
.
Пусть E
— середина KL
. Тогда окружность S_{1}
касается KL
в точке E
.
Прямоугольные треугольники O_{1}PI
и O_{1}EK
равны по катету (O_{1}P=O_{1}E
как радиусы окружности S_{1}
) и гипотенузе (O_{1}I=O_{1}K
по доказанному). Поэтому
\angle O_{1}IP=\angle O_{1}KE=\alpha=\angle O_{1}MK.
Следовательно, IP\parallel KM
.
Аналогично, IQ\parallel KM
. Следовательно, точки Q
, I
, P
лежат на одной прямой, параллельной KM
.
Аналогично докажем, что общая касательная к окружностям S_{3}
и S_{4}
, отличная от CD
, также параллельна KM
, а значит, эти две касательные параллельны.
Аналогично докажем, что общие касательные к окружностям S_{1}
и S_{4}
, S_{2}
и S_{3}
отличные соответственно от прямых AD
и BC
, также параллельны.
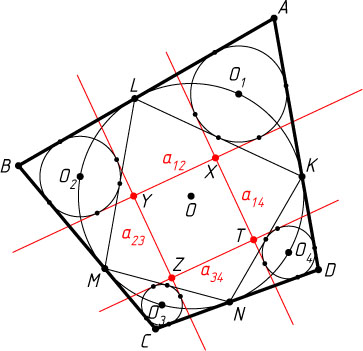
Таким образом, четырёхугольник XYZT
(рис. 3), о котором говорится в условии задачи, — параллелограмм.
3) Докажем, что XYZT
— ромб. Пусть a_{ij}
— длина общей касательной к окружностям S_{ij}
. Отрезки касательных, проведённых к окружности S_{1}
из вершины A
, равны между собой. Также равны между собой отрезки касательных, проведённых к окружности S_{1}
из точки X
. Аналогично для остальных вершин четырёхугольников ABCD
и XYZT
. Поскольку четырёхугольник ABCD
— описанный, то AB+CD=AD+BC
. Поэтому
(a_{12}+a_{34})-(a_{23}+a_{41})=AB+CD-(AD+BC)=0,
(XY+ZT)-(YZ+XT)=(a_{12}+a_{34})-(a_{23}+a_{41})=0.
Значит, XY+ZT=YZ+XT
. Следовательно, XYZT
— ромб.
Автор: Сонкин М. Г.
Источник: Всероссийская олимпиада школьников. — 1998-99, XXV, заключительный этап, 11 класс
Источник: Журнал «Квант». — 1999, № 5, с. 51
Источник: Агаханов Н. Х. и др. Всероссийские математические олимпиады школьников. 1993—2006. — М.: МЦНМО, 2007. — № 587, с. 76


