6533. В равнобедренном треугольнике ABC
(AB=BC
) проведена биссектриса CD
. Прямая, перпендикулярная CD
и проходящая через центр описанной около треугольника ABC
окружности, пересекает BC
в точке E
. Прямая, проходящая через точку E
параллельно CD
, пересекает AB
в точке F
. Докажите, что BE=FD
.
Решение. Заметим, что для равностороннего треугольника утверждение очевидно. Пусть биссектриса CD
пересекает высоту BM
треугольника ABC
в точке K
отличной от центра O
описанной окружности треугольника ABC
.
Рассмотрим случай, когда точка O
лежит на отрезке BK
. Положим \angle BCA=\angle BAC=2\alpha
. Пусть прямая OE
пересекает биссектрису CD
в точке P
. Тогда
\angle ECK=\angle MCK=\alpha,~\angle CKM=90^{\circ}-\alpha,
\angle BOE=\angle KOP=90^{\circ}-\angle OKP=90^{\circ}-\angle CKM=\alpha=\angle ECK.
Значит, \angle ECK+\angle EOK=180^{\circ}
. Поэтому точки C
, E
, O
и K
лежат на одной окружности. Вписанные углы OKE
и OCE
этой окружности опираются на одну и ту же дугу, поэтому они равны, а так как \angle ABM=\angle CBM=90^{\circ}-2\alpha
и треугольник BOC
равнобедренный, то
\angle OKE=\angle OCE=\angle OCB=\angle CBO=\angle OBA.
Значит, прямые EK
и AB
параллельны. Таким образом, противоположные стороны четырёхугольника EFDK
попарно параллельны. Поэтому EFDK
— параллелограмм. Следовательно, DF=EK
, а так как \angle KBE=\angle BKE
, то BE=EK=DF
, что и требовалось доказать.
Аналогично для случая, когда точка O
лежит вне отрезка BK
.
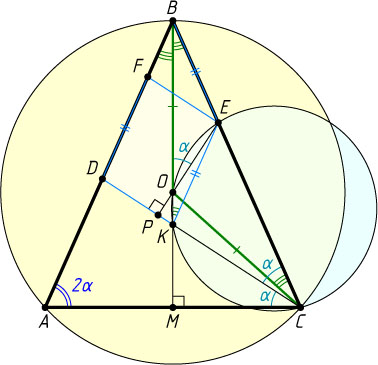
Автор: Сонкин М. Г.
Источник: Всероссийская олимпиада школьников. — 1995-96, XXII, заключительный этап, 11 кл.
Источник: Журнал «Квант». — 1996, № 5, с. 53
Источник: Агаханов Н. Х. и др. Всероссийские математические олимпиады школьников. 1993—2006. — М.: МЦНМО, 2007. — № 518, с. 67
