6539. Дан четырёхугольник ABCD
, в котором AB=AD
и \angle ABC=\angle ADC=90^{\circ}
. На сторонах BC
и CD
выбраны соответственно точки F
и E
так, что DF\perp AE
. Докажите, что AF\perp BE
.
Указание. Примените скалярное произведение векторов.
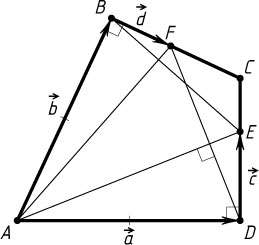
Решение. Обозначим \overrightarrow{AD}=\overrightarrow{a}
, \overrightarrow{AB}=\overrightarrow{b}
\overrightarrow{DE}=\overrightarrow{c}
и \overrightarrow{BF}=\overrightarrow{d}
. Тогда
\overrightarrow{DF}=\overrightarrow{b}+\overrightarrow{d}-\overrightarrow{a},~\overrightarrow{AE}=\overrightarrow{a}+\overrightarrow{c},~\overrightarrow{AF}=\overrightarrow{b}+\overrightarrow{d},~\overrightarrow{BE}=\overrightarrow{a}+\overrightarrow{c}-\overrightarrow{b}.
По условию DF\perp AE
и AD\perp DE
, поэтому
(\overrightarrow{b}+\overrightarrow{d}-\overrightarrow{a})(\overrightarrow{a}+\overrightarrow{c})=0.
Значит,
(\overrightarrow{b}+\overrightarrow{d})(\overrightarrow{a}+\overrightarrow{c})-\overrightarrow{a}(\overrightarrow{a}+\overrightarrow{c})=(\overrightarrow{b}+\overrightarrow{d})(\overrightarrow{a}+\overrightarrow{c})-|\overrightarrow{a}|^{2}-\overrightarrow{a}\cdot\overrightarrow{c}=
=(\overrightarrow{b}+\overrightarrow{d})(\overrightarrow{a}+\overrightarrow{c})-|\overrightarrow{a}|^{2}=0.
Поскольку AB\perp BF
, а |\overrightarrow{b}|=AB=AD=|\overrightarrow{a}|
, то
\overrightarrow{AF}\cdot\overrightarrow{BE}=(\overrightarrow{b}+\overrightarrow{d})(\overrightarrow{a}+\overrightarrow{c}-\overrightarrow{b})=(\overrightarrow{b}+\overrightarrow{d})(\overrightarrow{a}+\overrightarrow{c})-|\overrightarrow{b}|^{2}=
=(\overrightarrow{b}+\overrightarrow{d})(\overrightarrow{a}+\overrightarrow{c})-|\overrightarrow{a}|^{2}=0.
Следовательно, AF\perp BE
.
Автор: Сонкин М. Г.
Источник: Всероссийская олимпиада школьников. — 1994-95, XXI, окружной этап, 10 класс
Источник: Журнал «Квант». — 1995, № 5, с. 47
Источник: Агаханов Н. Х. и др. Всероссийские математические олимпиады школьников. 1993—2006. — М.: МЦНМО, 2007. — № 3, с. 14
