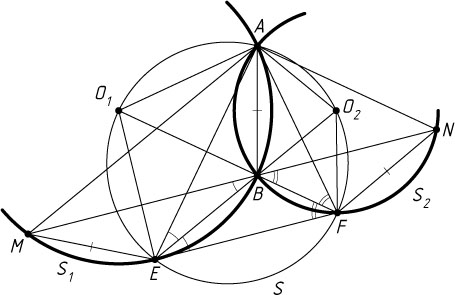
6540. Окружности S_{1}
и S_{2}
с центрами O_{1}
и O_{2}
пересекаются в точках A
и B
. Луч O_{1}B
пересекает окружность S_{2}
в точке F
, а луч O_{2}B
пересекает окружность S_{1}
в точке E
. Прямая, проходящая через точку B
параллельно прямой EF
, вторично пересекает окружности S_{1}
и S_{2}
в точках M
и N
соответственно. Докажите, что MN=AE+AF
.
Указание. Точки A
, E
, F
, O_{1}
и O_{2}
лежат на одной окружности.
Решение. Заметим, что BEO_{1}
и BFO_{2}
— углы при основаниях BE
и BF
равнобедренных треугольников BEO_{1}
и BFO_{2}
. Из равенства вертикальных углов O_{1}BE
и O_{2}BF
следует, что
\angle O_{1}EO_{2}=\angle O_{1}EB=\angle O_{1}BE=\angle O_{2}BF=\angle BFO_{2}=\angle O_{1}FO_{2}.
Значит, из точек E
и F
, лежащих по одну сторону от прямой O_{1}O_{2}
, отрезок O_{1}O_{2}
виден под одним и тем же углом. Поэтому точки E
, F
, O_{1}
, O_{2}
лежат на одной окружности. Обозначим её S
.
Из равенства по трём сторонам треугольников O_{1}BO_{2}
и O_{1}AO_{2}
следует равенство углов O_{1}BO_{2}
и O_{1}AO_{2}
. Поэтому
\angle O_{1}AO_{2}+\angle O_{1}EO_{2}=\angle O_{1}BO_{2}+\angle O_{1}EB=\angle O_{1}BO_{2}+\angle O_{1}BE=180^{\circ}.
Значит, точки E
, A
, O_{1}
, O_{2}
лежат на одной окружности, а так как через через точки E
, O_{1}
и O_{2}
, не лежащие на одной прямой, проходит единственная окружность S
, то на этой окружности лежат все пять точек A
, E
, F
, O_{1}
и O_{2}
.
Вписанные в окружность S
углы FEO_{2}
и AEO_{2}
опираются на равные хорды O_{2}F
и O_{2}A
(радиусы окружности S_{2}
), поэтому \angle FEO_{2}=\angle AEO_{2}
. С другой стороны, поскольку EF\parallel MB
, то \angle FEO_{2}=\angle MBE
, значит,
\angle AEB=\angle AEO_{2}=\angle FEO_{2}=\angle MBE.
Вписанные в окружность S_{1}
равные углы MBE
и AEB
опираются на равные хорды ME
и AB
. Поэтому ABEM
— равнобедренная трапеция. Её диагонали равны, т. е. AE=MB
.
Аналогично докажем, что AF=BN
. Следовательно,
MN=MB+BN=AE+AF.
Автор: Сонкин М. Г.
Источник: Всероссийская олимпиада школьников. — 1994-95, XXI, окружной этап, 11 класс
Источник: Журнал «Квант». — 1995, № 5, с. 47
Источник: Агаханов Н. Х. и др. Всероссийские математические олимпиады школьников. 1993—2006. — М.: МЦНМО, 2007. — № 71, с. 15
