6542. Точки A_{2}
, B_{2}
и C_{2}
— середины высот AA_{1}
, BB_{1}
и CC_{1}
остроугольного треугольника ABC
. Найдите сумму углов B_{2}A_{1}C_{2}
, C_{2}B_{1}A_{2}
и A_{2}C_{1}B_{2}
.
Ответ. 180^{\circ}
.
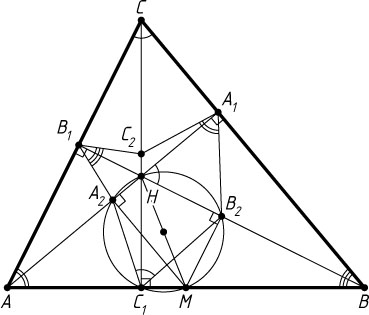
Указание. Пусть H
— точка пересечения высот треугольника ABC
, M
— середина стороны AB
. Докажите, что точки H
, M
, B_{2}
, A_{2}
и C_{1}
лежат на одной окружности.
Решение. Пусть H
— точка пересечения высот треугольника ABC
, M
— середина стороны AB
. Поскольку MB_{2}
и MA_{2}
— средние линии прямоугольных треугольников AB_{1}B
и AA_{1}B
, то
\angle MB_{2}H=\angle AB_{1}B=90^{\circ},~\angle MA_{2}H=\angle BA_{1}A=90^{\circ},
поэтому из точек B_{2}
, A_{2}
и C_{1}
отрезок MH
виден под прямым углом. Значит, эти точки лежат на окружности с диаметром MH
. Четырёхугольник A_{2}C_{1}B_{2}H
— вписанный, поэтому
\angle A_{2}C_{1}B_{2}=180^{\circ}-\angle A_{2}HB_{2}=180^{\circ}-\angle A_{1}HB_{1}=\angle ACB.
Аналогично докажем, что
\angle B_{2}A_{1}C_{2}=\angle BAC,~\angle C_{2}B_{1}A_{2}=\angle ABC.
Следовательно,
\angle A_{2}C_{1}B_{2}+\angle B_{2}A_{1}C_{2}+\angle C_{2}B_{1}A_{2}=\angle ACB+\angle BAC+\angle ABC=180^{\circ}.
Автор: Терёшин Д. А.
Источник: Всероссийская олимпиада школьников. — 1994-95, XXI, заключительный этап, 9 класс
Источник: Журнал «Квант». — 1995, № 5, с. 47
Источник: Агаханов Н. Х. и др. Всероссийские математические олимпиады школьников. 1993—2006. — М.: МЦНМО, 2007. — № 478, с. 62
