6543. Даны полуокружность с диаметром AB
и центром O
, а также прямая, пересекающая полуокружность в точках C
и D
, а прямую AB
— в точке M
(MB\lt MA
, MD\lt MC
). Пусть K
— отличная от O
точка пересечения окружностей, описанных около треугольников AOC
и DOB
. Докажите, что угол MKO
— прямой.
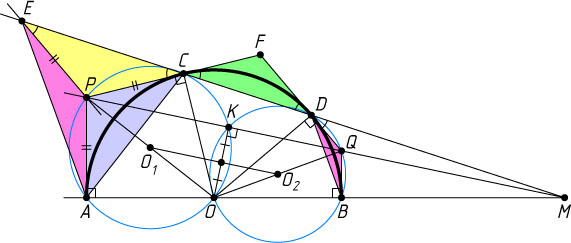
Решение. Пусть O_{1}
и O_{2}
центры описанных окружностей треугольников AOC
и DOB
соответственно, OP
— диаметр окружности с центром O_{1}
, OQ
— диаметр окружности с центром O_{2}
.
Тогда O_{1}O_{2}
— серединный перпендикуляр к общей хорде OK
. Значит, O_{1}O_{2}\perp OK
и O_{1}O_{2}
проходит через середину OK
.
Поскольку OP
и OQ
— диаметры окружностей, то
\angle OKP=\angle OKQ=90^{\circ}.
Поэтому точка K
лежит на отрезке PQ
и OK\perp PQ
. Таким образом достаточно доказать, что точка M
лежит на прямой PQ
.
Поскольку точка A
лежит на окружности с диаметром OP
, то AP\perp OA
, поэтому AP
— касательная к данной полуокружности. Аналогично, PC
, QB
и QD
— также касательные к полуокружности.
Пусть F
— точка пересечения прямых PC
и QD
, а E
— точка пересечения прямой CD
с прямой, проходящей через точку P
параллельно QD
. По теореме о равенстве отрезков касательных, проведённых к окружности из одной точки
FC=FD,~QD=QB,~PC=PA.
Значит, треугольники DFC
, BQD
и APC
— равнобедренные. Поэтому
\angle QDM=\angle FDC=\angle FCD=\angle PCE,
а так как PE\parallel QD
, то
\angle PEC=\angle QDM=\angle PCE.
Значит, треугольник CPE
— равнобедренный, PC=PE
. Поэтому PA=PC=PE
. Следовательно, треугольник APE
— также равнобедренный.
Таким образом, о равнобедренных треугольниках BQD
и APE
известно, что PE\parallel QD
и AP\parallel BQ
. Значит,
\angle PAE=\frac{1}{2}(180^{\circ}-\angle APE)=\frac{1}{2}(180^{\circ}-\angle BQD)=\angle QBD.
Тогда при гомотетии с центром в точке M
и коэффициентом \frac{MA}{MB}
точка B
перейдёт в точку A
, точка D
— в точку E
, луч BQ
— в луч AP
, луч DQ
— в луч EP
, а значит, точка Q
— в точку P
. Следовательно, прямая PQ
проходит через центр гомотетии — точку M
. Что и требовалось доказать.
Автор: Купцов Л. П.
Источник: Всероссийская олимпиада школьников. — 1994-95, XXI, заключительный этап, 10 класс
Источник: Журнал «Квант». — 1995, № 5, с. 48
Источник: Агаханов Н. Х. и др. Всероссийские математические олимпиады школьников. 1993—2006. — М.: МЦНМО, 2007. — № 486, с. 63
