6544. В треугольнике ABC
провели биссектрисы углов A
и C
. Точки P
и Q
— основания перпендикуляров, опущенных из вершины B
на эти биссектрисы. Докажите, что отрезок PQ
параллелен стороне AC
.
Указание. Продолжите указанные перпендикуляры до пересечения с прямой AC
.
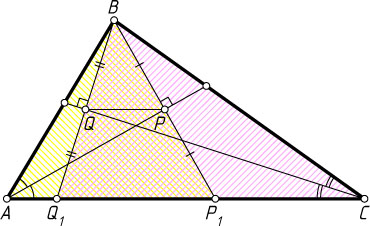
Решение. Пусть точка P
лежит на биссектрисе угла A
, а точка Q
— на биссектрисе угла C
. Продолжим перпендикуляры BP
и BQ
до пересечения с прямой AC
в точках P_{1}
и Q_{1}
соответственно. Тогда биссектриса, проведённая из вершины A
треугольника ABP_{1}
, является его высотой. Значит, треугольник ABP_{1}
— равнобедренный. Его биссектриса AP
является медианой. Значит, P
— середина BP_{1}
. Аналогично докажем, что Q
— середина BQ_{1}
. Тогда PQ
— средняя линия треугольника P_{1}BQ_{1}
, поэтому PQ\parallel P_{1}Q_{1}
. Следовательно, PQ\parallel AC
.
