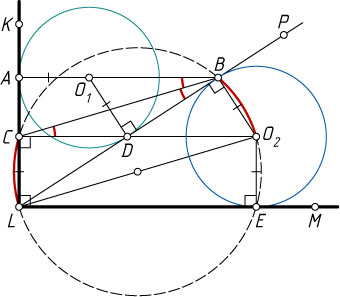
6546. Внутри прямого угла KLM
взята точка P
. Окружность S_{1}
с центром O_{1}
касается сторон LK
и LP
угла KLP
в точках A
и D
соответственно, а окружность S_{2}
с центром O_{2}
такого же радиуса касается сторон угла MLP
, причём стороны LP
— в точке B
. Оказалось, что точка O_{1}
лежит на отрезке AB
. Пусть C
— точка пересечения прямых O_{2}D
и KL
. Докажите, что BC
— биссектриса угла ABD
.
Решение. Поскольку O_{1}D=O_{2}B
(как радиусы равных окружностей) и O_{1}D\parallel O_{2}B
(как перпендикуляры к прямой LP
), то DO_{1}BO_{2}
— параллелограмм, поэтому CO_{2}\parallel AB\parallel LE
, где E
— точка касания окружности S_{2}
с прямой LM
. Значит, CLEO_{2}
— прямоугольник. Поэтому CL=O_{2}E=O_{2}B
.
Из точек C
и B
отрезок LO_{2}
виден под прямым углом, значит, эти точки лежат на окружности с диаметром LO_{2}
. Вписанные углы CBL
и BCO_{2}
этой окружности опираются на равные хорды CL
и O_{2}B
этой окружности, поэтому \angle CBL=\angle BCO_{2}
, а так как CO_{2}\parallel AB
, то
\angle CBL=\angle BCO_{2}=\angle ABC.
Следовательно, BC
— биссектриса угла ABD
.
Автор: Кочерова А. С.
Источник: Всероссийская олимпиада школьников. — 1993-94, XX, окружной этап, 9 класс
Источник: Журнал «Квант». — 1994, № 5, с. 52
Источник: Агаханов Н. Х. и др. Всероссийские математические олимпиады школьников. 1993—2006. — М.: МЦНМО, 2007. — № 30, с. 10
