6549. Окружность с центром O
вписана в треугольник ABC
и касается его сторон AB
, BC
и AC
в точках E
, F
и D
соответственно. Прямые AO
и CO
пересекают прямую EF
в точках M
и N
. Докажите, что центр окружности, описанной около треугольника OMN
, точка O
и точка D
лежат на одной прямой.
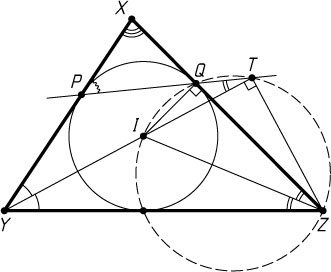
Решение. Лемма. Пусть P
и Q
точки касания со сторонами соответственно XY
и XZ
окружности с центром I
, вписанной в треугольник XYZ
; T
— точка пересечения прямых YI
и PQ
. Тогда \angle YTZ=90^{\circ}
.
Доказательство. Пусть точка T
(рис. 1) лежит вне отрезка PQ
(например, на продолжении PQ
за точку Q
). Обозначим углы треугольника XYZ
через \alpha
, \beta
и \gamma
. Из равнобедренного треугольника XPQ
находим, что
\angle XPT=\angle XPQ=90^{\circ}-\frac{\alpha}{2}.
Поскольку XPT
— внешний угол треугольника YPT
, то
\angle YTP=\angle XPT-\angle PYT=90^{\circ}-\frac{\alpha}{2}-\frac{\beta}{2}=\frac{\gamma}{2}=\angle IZQ.
Из точек T
и Z
, лежащих по одну сторону от прямой IQ
, отрезок IQ
виден под одним и тем же углом, равным \frac{\gamma}{2}
. Значит, эти точки лежат на одной окружности, а так как вписанный в эту окружность угол IQZ
— прямой, то IZ
— диаметр окружности. Следовательно,
\angle YTZ=\angle ITZ=90^{\circ}.
Аналогично для случая, когда точка T
лежит на отрезке PQ
.
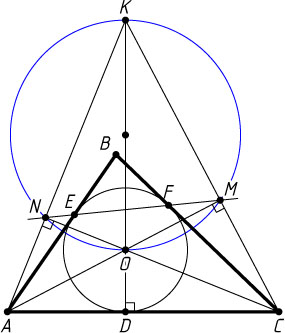
Перейдём к нашей задаче (рис. 2). Пусть прямые AO
и CO
пересекают прямую EF
в точках M
и N
соответственно. Продолжим отрезки AN
и CM
до пересечения в точке K
. По доказанной лемме CN\perp AN
и AM\perp CM
, поэтому CN
и AM
— высоты треугольника AKC
, а O
— точка их пересечения. Поскольку OD\perp AC
, то точка D
— основание третьей высоты треугольника AKC
.
Из точек N
и M
отрезок OK
виден под прямым углом, значит, эти точки лежат на окружности с диаметром OK
. Поэтому центр этой окружности лежит на прямой KD
. Поскольку эта окружность является описанной окружностью треугольника OMN
, то утверждение доказано.
Автор: Сонкин М. Г.
Источник: Всероссийская олимпиада школьников. — 1993-94, XX, окружной этап, 11 класс
Источник: Журнал «Квант». — 1994, № 5, с. 53
Источник: Агаханов Н. Х. и др. Всероссийские математические олимпиады школьников. 1993—2006. — М.: МЦНМО, 2007. — № 43, с. 12

