6553. В треугольнике ABC
угол C
— прямой. На стороне AC
нашлась точка D
, а на отрезке BD
— точка K
такие, что \angle ABC=\angle KAD=\angle AKD
. Докажите, что BK=2DC
.
Решение. Обозначим
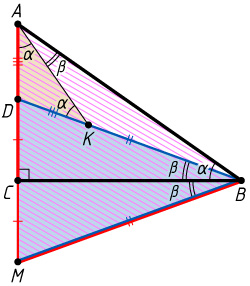
\angle ABC=\angle KAD=\angle AKD=\alpha,~\angle BAK=\beta.
На продолжении отрезка DC
за точку C
отложим отрезок CM=DC
. Тогда высота BC
треугольника DBM
является его медианой, поэтому треугольник DBM
— равнобедренный с основанием DM
.
Поскольку AKD
— внешний угол треугольника ABK
, то
\angle ABK=\angle AKD-\angle BAK=\alpha-\beta.
Тогда
\angle CBD=\angle ABC-\angle ABK=\alpha-(\alpha-\beta)=\beta,
\angle CBM=\angle CBD=\beta,~\angle ABM=\angle ABC+\angle CBM=\alpha+\beta=\angle BAM.
Значит, треугольник ABM
— равнобедренный с основанием AB
, BM=AM=BD
и, кроме того, DK=AD
. Следовательно,
BK=BD-DK=BM-DK=AM-AD=DM=2DC,
что и требовалось доказать
Автор: Иванов С. В.
Источник: Всероссийская олимпиада школьников. — 2002-03, XXIX, окружной этап, 8 класс
Источник: Журнал «Квант». — 2003, № 5, с. 44
Источник: Агаханов Н. Х. и др. Всероссийские математические олимпиады школьников. 1993—2006. — М.: МЦНМО, 2007. — № 303, с. 43
