6559. Три окружности \omega_{1}
, \omega_{2}
и \omega_{3}
радиуса r
проходят через точку S
и касаются внутренним образом окружности \omega
радиуса R
(R\gt r
) в точках T_{1}
, T_{2}
и T_{3}
соответственно. Докажите, что прямая T_{1}T_{2}
проходит через вторую (отличную от S
) точку пересечения окружностей \omega_{1}
и \omega_{2}
.
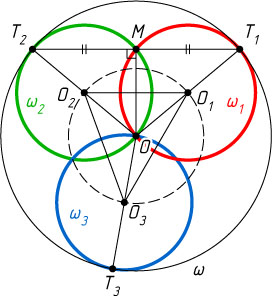
Решение. Обозначим через O_{1}
, O_{2}
, O_{3}
и O
центры окружностей \omega_{1}
, \omega_{2}
, \omega_{3}
и \omega
соответственно. Поскольку линия центров двух касающихся окружностей проходит через их точку касания, то точки O
, O_{1}
и T_{1}
лежат на одной прямой, причём
OO_{1}=OT_{1}-O_{1}T_{1}=R-r.
Аналогично,
OO_{2}=OO_{3}=R-r,
поэтому O
— центр окружности, описанной около треугольника O_{1}O_{2}O_{3}
. Поскольку
SO_{1}=SO_{2}=SO_{3}=r,
точка S
также является центром окружности, описанной около треугольника O_{1}O_{2}O_{3}
. Следовательно, точки S
и O
совпадают.
Пусть M
— середина отрезка T_{1}T_{2}
. Тогда OM
— медиана и высота равнобедренного треугольника OT_{1}T_{2}
. Значит, точка M
лежит на окружности с диаметром OT_{1}
, т. е. M
лежит на окружности \omega_{1}
. Аналогично, M
лежит на \omega_{2}
. Отсюда следует утверждение задачи.
Автор: Емельянова Т. Л.
Источник: Всероссийская олимпиада школьников. — 2004, XXX, окружной этап, 11 класс
Источник: Журнал «Квант». — 2004, № 5, с. 45, задача 2, 11 класс
Источник: Агаханов Н. Х. и др. Всероссийские математические олимпиады школьников. 1993—2006. — М.: МЦНМО, 2007. — № 354, с. 48
