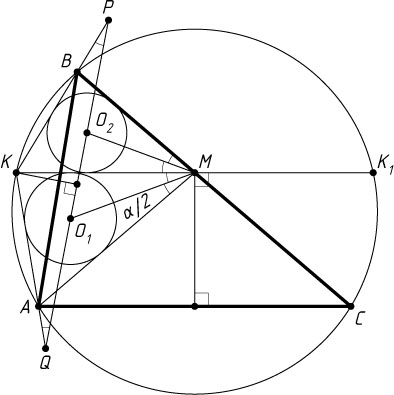
6564. Серединный перпендикуляр к стороне AC
треугольника ABC
пересекает сторону BC
в точке M
. Биссектриса угла AMB
пересекает описанную окружность треугольника ABC
в точке K
. Докажите, что прямая, проходящая через центры вписанных окружностей треугольников AKM
и BKM
, перпендикулярна биссектрисе угла AKB
.
Решение. Поскольку MK
— биссектриса внешнего угла при вершине M
равнобедренного треугольника AMC
, то MK\parallel AC
. Пусть продолжение отрезка MK
за точку M
пересекает описанную окружность треугольника ABC
в точке K_{1}
. Тогда дуги AK
и CK_{1}
, заключённые между параллельными хордами KK_{1}
и AC
, равны. Поэтому
\angle KBM=\angle KBC=\angle AKK_{1}=\angle AKM.
Тогда треугольники MAK
подобен треугольнику MKB
по двум углам.
Если \angle BMK=\angle KMA=\alpha
, то треугольник MAK
переходит в треугольник MKB
при композиции поворота вокруг точки M
на угол \alpha
и гомотетии с центром M
(поворотной гомотетии с центром M
и углом \alpha
). При этом центр O_{1}
вписанной окружности треугольника MAK
переходит в центр O_{2}
вписанной окружности треугольника MKB
.
Поскольку
\frac{MO_{1}}{MO_{2}}=\frac{MK}{MB}~\mbox{и}~\angle O_{1}MO_{2}=\angle O_{1}MK+\angle O_{2}MK=\frac{\alpha}{2}+\frac{\alpha}{2}=\alpha=\angle KMB,
то треугольник O_{1}MO_{2}
подобен треугольнику KMB
и переходит в него при композиции поворота на угол \frac{\alpha}{2}
вокруг точки M
и гомотетии с центром M
. Тогда угол между прямыми O_{1}O_{2}
и KB
также равен \frac{\alpha}{2}
. Аналогично, угол между прямыми O_{1}O_{2}
и KA
равен \frac{\alpha}{2}
.
Если прямая O_{1}O_{2}
пересекает прямые KB
и KA
в точках P
и Q
, то треугольник PKQ
— равнобедренный. Его биссектриса, проведённая из вершины K
, является высотой, а значит, перпендикулярна прямой O_{1}O_{2}
.
Автор: Берлов С. Л.
Источник: Всероссийская олимпиада школьников. — 2001-02, XXVIII, окружной этап, 10 класс
Источник: Журнал «Квант». — 2002, № 5, с. 49
Источник: Агаханов Н. Х. и др. Всероссийские математические олимпиады школьников. 1993—2006. — М.: МЦНМО, 2007. — № 283, с. 40
