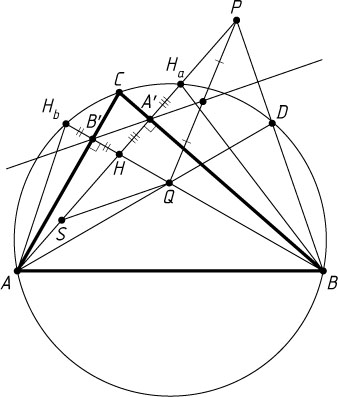
6572. В остроугольном треугольнике проведены высоты AA'
и BB'
. На дуге ACB
описанной окружности треугольника ABC
выбрана точка D
. Пусть прямые AA'
и BD
пересекаются в точке P
, а прямые BB'
и AD
пересекаются в точке Q
. Докажите, что прямая A'B'
проходит через середину отрезка PQ
.
Решение. Пусть, для определённости, точка D
лежит на дуге BC
, не содержащей точку A
. Обозначим через H
— точку пересечения высот треугольника ABC
, а через H_{A}
и H_{B}
— вторые точки пересечения прямых AH
и BH
с окружностью.
Поскольку точка, симметричная ортоцентру относительно стороны треугольника, лежит на описанной окружности треугольника, то HA'=A'H_{A}
и HB'=B'H_{B}
. Прямоугольный треугольник H_{A}A'B
равен треугольнику HA'B
, а треугольник HA'B
подобен треугольнику HB'A
, значит, треугольник H_{A}A'B
подобен треугольнику HB'A
.
Из равенств
\angle B'AQ=\angle CAD=\angle CBD=\angle A'BP
следует, что отрезки AQ
и BP
являются соответствующими в подобных треугольниках HB'A
и H_{A}A'B
, поэтому \frac{B'Q}{B'H}=\frac{A'P}{A'H_{A}}
.
Пусть прямая, проходящая через точку Q
параллельно A'B'
, пересекает прямую AA'
в точке S
. Тогда по теореме о пропорциональных отрезках
\frac{A'S}{A'H}=\frac{B'Q}{B'H}=\frac{A'P}{A'H_{A}}=\frac{A'P}{A'H}.
Значит, A'S=A'P
, т. е. A'
— середина SP
, а так как A'B'\parallel QS
, то прямая A'B'
проходит через середину отрезка PQ
.
Автор: Акопян А. В.
Источник: Всероссийская олимпиада школьников. — 2004-05, XXXI, заключительный этап, 9 класс
Источник: Журнал «Квант». — 2005, № 5, с. 46
Источник: Агаханов Н. Х. и др. Всероссийские математические олимпиады школьников. 1993—2006. — М.: МЦНМО, 2007. — № 719, с. 93
