6592. Окружности S_{1}
и S_{2}
пересекаются в точках M
и N
. Через точку A
окружности S_{1}
проведены прямые AM
и AN
, пересекающие окружность S_{2}
в точках B
и C
, а через точку D
окружности S_{2}
— прямые DM
и DN
, пересекающие S_{1}
в точках E
и F
, причём точки A
, E
, F
лежат по одну сторону от прямой MN
, а D
, B
, C
— по другую (см.рис.). Докажите, что если AB=DE
, то точки A
, F
, C
и D
лежат на одной окружности, положение центра которой не зависит от выбора точек A
и D
.
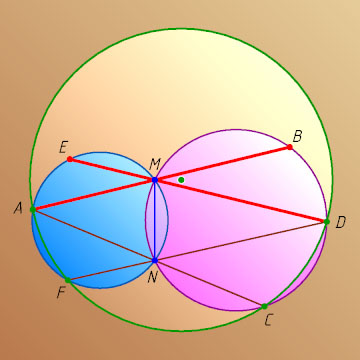
Решение. Лемма (теорема Н. И. Фусса). Пусть окружности S_{1}
и S_{2}
пересекаются в точках M
и N
. Через точку M
проведена прямая, пересекающая S_{1}
в точке E
, S_{2}
— в точке D
, а через точку N
— прямая, пересекающая S_{1}
в точке A
, S_{2}
— в точке C
. Тогда AE\parallel CD
.
Доказательство. Рассмотрим случай, изображённый на рис. 1, который соответствует условию, решаемой задачи. В остальных случаях доказательство проводится аналогично.
Из вписанных четырёхугольников ANME
и NCDM
получаем, что
\angle AEM=180^{\circ}-\angle ANM=\angle MNC=180^{\circ}-\angle MDC,
т. е. \angle AEM+\angle MDC=180^{\circ}
. Следовательно, AE\parallel CD
. Лемма доказана.
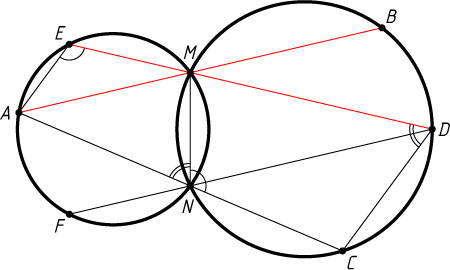
Перейдём к решению задачи, обратившись к рис. 2.
По теореме о вписанных углах
\angle NAB=\angle NAM=\angle NEM=\angle NED,
\angle NBA=\angle NBM=\angle NDM=\angle NDE,
а так как AB=DE
, то треугольники ANB
и END
равны по стороне и двум прилежащим к ней углам.
Пусть NK
и NL
— диаметры окружностей S_{1}
и S_{2}
соответственно. Тогда \angle KMN=\angle LMN=90^{\circ}
, т. е. точки K
, M
и L
лежат на одной прямой, перпендикулярной MN
.
Из равенства прямоугольных треугольников NAK
и NEK
по катету (NA=NE
из равенства треугольников ANB
и END
) и общей гипотенузе NK
следует равенство углов ANK
и ENK
. Аналогично, \angle DNL=\angle BNL
. Значит,
\angle AMK=\angle BML=\angle DML,~\angle AMN=90^{\circ}-\angle AMK=90^{\circ}-\angle DML=\angle DMN.
Из вписанных четырёхугольников AFNM
и DCNM
получаем, что
\angle AFD=\angle AFN=180^{\circ}-\angle AMN=180^{\circ}-\angle DMN=\angle DCN=\angle DCA.
Следовательно, точки A
, F
, C
и D
лежат на одной окружности,
Докажем, что центр этой окружности — середина отрезка KL
. Пусть прямая KN
вторично пересекает окружность S_{2}
в точке P
, а прямая LN
вторично пересекает окружность S_{1}
в точке T
.
Из равенства прямоугольных треугольников NAK
и NEK
следует, что точки A
и E
симметричны относительно прямой KP
, поэтому KP\perp AE
, а так как AE\parallel CD
(по лемме), то KP\perp CD
. Поскольку NP\perp PL
(NL
— диаметр окружности S_{2}
), то PL\parallel CD
. Значит, серединные перпендикуляры к параллельным хордам PL
и CD
совпадают. Аналогично докажем, что совпадают серединные перпендикуляры к отрезкам AF
и KT
.
Поскольку KL
— общая гипотенуза прямоугольных треугольников KPL
и KTL
, а серединный перпендикуляр к катету проходит через середину гипотенузы, то серединные перпендикуляры к сторонам AF
и CD
вписанного четырёхугольника AFCD
пересекаются в середине отрезка KL
. Что и требовалось доказать.
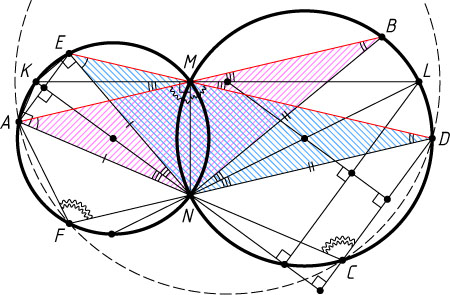
Примечание. Утверждение задачи остаётся справедливым, даже если в условии отказаться от уточнения взаимного расположения точек A
, E
, F
, D
, B
, C
(см.мультфильм).
Автор: Сонкин М. Г.
Автор: Терёшин Д. А.
Источник: Всероссийская олимпиада школьников. — 1999-2000, XXVI, окружной этап, 9 класс
Источник: Журнал «Квант». — 2000, № 5, с. 50
Источник: Агаханов Н. Х. и др. Всероссийские математические олимпиады школьников. 1993—2006. — М.: МЦНМО, 2007. — № 212, с. 32


