6613. Пусть точки A
, B
, C
лежат на окружности, а прямая b
касается этой окружности в точке B
. Из точки P
, лежащей на прямой b
, опущены перпендикуляры PA_{1}
и PC_{1}
на прямые AB
и BC
соответственно (точки A_{1}
и C_{1}
лежат на отрезках AB
и BC
). Докажите, что A_{1}C_{1}\perp AC
.
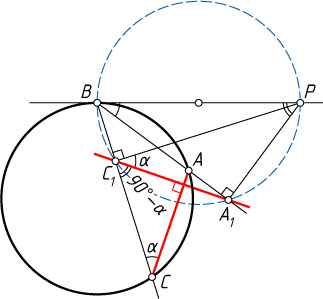
Решение. Рассмотрим случай, когда 90^{\circ}\gt\angle PBC\gt\angle PBA
.
Из точек A_{1}
и C_{1}
отрезок BP
виден под прямым углом, значит, эти точки лежат на окружности с диаметром BP
. Вписанные в эту окружность углы A_{1}C_{1}P
и A_{1}BP
опираются на одну и ту же дугу, поэтому \angle A_{1}C_{1}P=\angle A_{1}BP
.
Обозначим \angle A_{1}C_{1}P=\angle A_{1}BP=\alpha
. Из теоремы об угле между касательной и хордой следует, что
\angle ACB=\angle ABP=\angle A_{1}BP=\alpha.
С другой стороны
\angle A_{1}C_{1}C=180^{\circ}-\angle BC_{1}A_{1}=\angle BPA_{1}=90^{\circ}-\angle A_{1}BP=90^{\circ}-\alpha.
Следовательно,
\angle ACC_{1}+\angle A_{1}C_{1}C=\angle ACB+\angle A_{1}C_{1}C=\alpha+90^{\circ}-\alpha=90^{\circ},
т. е. A_{1}C_{1}\perp AC
.
Аналогично для других случаев.
Автор: Емельянов Л. А.
Источник: Всероссийская олимпиада школьников. — 2009-10, XXXVI, региональный этап, 9 класс
Источник: Журнал «Квант». — 2010, № 2, с. 54
