6614. Прямые, касающиеся окружности \omega
в точках B
и D
, пересекаются в точке P
. Прямая, проходящая через точку P
, высекает на окружности хорду AC
. Через произвольную точку отрезка AC
проведена прямая, параллельная BD
. Докажите, что она делит длины ломаных ABC
и ADC
в одинаковых отношениях.
Решение. Из теоремы об угле между касательной и хордой \angle ABP=\angle ACB=\angle PCB
, значит, треугольники ABP
и BCP
подобны по двум углам (угол при вершине P
— общий). Следовательно, \frac{AB}{BC}=\frac{BP}{CP}
. Аналогично, из подобия треугольников PDA
и PCD
следует, что \frac{AD}{CD}=\frac{DP}{CP}
, а так как BP=DP
, то \frac{AB}{BC}=\frac{AD}{CD}
, или \frac{AB}{AD}=\frac{BC}{CD}
. Тогда \frac{AB+BC}{AD+CD}=\frac{AB}{AD}=\frac{BC}{CD}
.
Пусть отрезки AC
и BD
пересекаются в точке Q
, а T
— произвольная точка отрезка AC
, причём для определённости точка T
лежит между Q
и C
, а прямая, проходящая через точку T
параллельно BD
, пересекает отрезки CB
и CD
в точках B'
и D'
соответственно. Тогда \frac{CB'}{CD'}=\frac{CB}{CD}=\frac{AB+CB}{AD+CD}
, или \frac{CB'}{AB+BC}=\frac{CD'}{AD+CD}
, что и требовалось доказать.
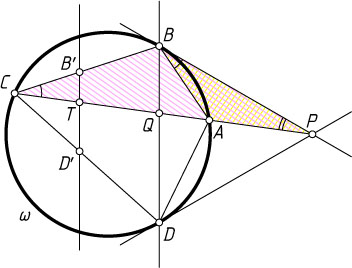
Автор: Емельянов Л. А.
Источник: Всероссийская олимпиада школьников. — 2009-10, XXXVI, региональный этап, 10 класс
Источник: Журнал «Квант». — 2010, № 2, с. 54
