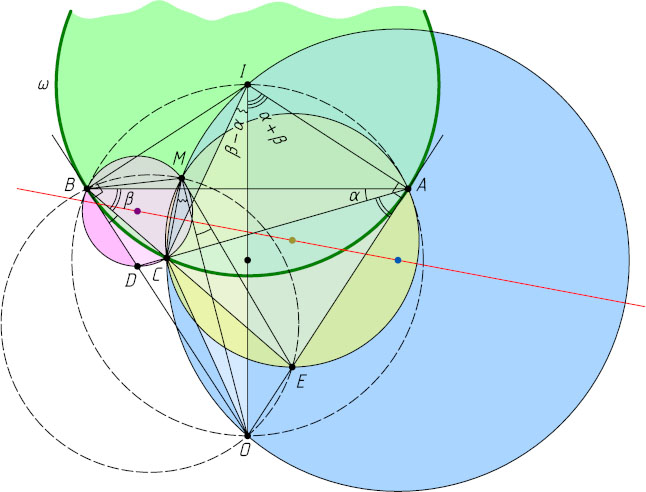
6618. Прямые, касающиеся окружности \omega
в точках A
и B
, пересекаются в точке O
. Точка I
— центр \omega
. На меньшей дуге AB
окружности \omega
выбрана точка C
, отличная от середины дуги. Прямые AC
и OB
пересекаются в точке D
, а прямые BC
и OA
— в точке E
. Докажите, что центры описанных окружностей треугольников ACE
, BCD
и OCI
лежат на одной прямой.
Решение. Обозначим \angle DAB=\alpha
, \angle ABC=\beta
. Предположим, что \alpha\lt\beta
. Заметим, что описанные окружности треугольников ACE
и BCD
пересекаются в двух точках (если бы они в точке C
касались, то из гомотетичности треугольников ACE
и DBC
следовало бы, что AE\parallel BD
).
Пусть M
— вторая общая точка описанных окружностей треугольников ACE
и DBC
. Для решения задачи достаточно доказать, что описанная окружность треугольника OCI
также проходит через точку M
(тогда центры трёх указанных в условии окружностей лежат на одной прямой — серединном перпендикуляре к отрезку CM
). В свою очередь, это будет следовать из того, что четырёхугольник OCMI
— вписанный.
Из теоремы об угле между касательной и хордой следует, что
\angle OAC=\angle ABC=\beta,~\angle OBC=\angle BAC=\alpha.
Из точек A
и B
отрезок OI
виден под прямым углом, значит, эти точки лежат на окружности с диаметром OI
. Вписанные в эту окружность углы AIO
и ABO
опираются на одну и ту же дугу, поэтому
\angle AIO=\angle ABO=\angle OBC+\angle ABC=\alpha+\beta,
а так как центральный угол AIC
окружности \omega
вдвое больше вписанного угла ABC
, то
\angle CIO=\angle AIC-\angle AIO=2\angle ABC-\angle AIO=2\beta-(\alpha+\beta)=\beta-\alpha.
Четырёхугольники AECM
и DBMC
— вписанные, поэтому
\angle BME=\angle BMC+\angle EMC=(180^{\circ}-\angle BDC)+\angle EAD=\angle ODA+\angle DAO=180^{\circ}-\angle EOB.
Значит, четырёхугольник EOBM
— также вписанный и \angle OME=\angle OBE=\alpha
, поэтому
\angle CMO=\angle CME-\angle OME=\angle CAE-\angle OBE=\beta-\alpha=\angle CIO.
Таким образом, из точек I
и M
отрезок OC
виден под одним и тем же углом. Следовательно, точки O
, I
, C
и M
лежат на одной окружности, что и требовалось доказать.
Автор: Полянский А. А.
Источник: Всероссийская олимпиада школьников. — 2009-10, XXXVI, заключительный этап, 9 класс
Источник: Журнал «Квант». — 2010, № 5, с. 50
