6619. Через центр O
окружности, описанной около неравнобедренного треугольника ABC
, проведены прямые, перпендикулярные сторонам AB
и AC
. Эти прямые пересекают высоту AD
треугольника ABC
в точках P
и Q
. Точка M
— середина стороны BC
, а S
— центр окружности, описанной около треугольника OPQ
. Докажите, что \angle BAS=\angle CAM
.
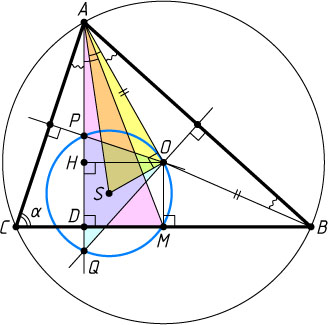
Решение. Рассмотрим случай, изображённый на рисунке (AB\gt AC
). Стороны треугольника OPQ
соответственно перпендикулярны сторонам треугольника ABC
(OP\perp AB
, OQ\perp AC
и PQ\perp BC
), значит, треугольник OPQ
подобен треугольнику ABC
с некоторым коэффициентом k
.
При этом подобии радиус SO
описанной окружности треугольника OPQ
соответствует радиусу AO
описанной окружности треугольника ABC
, поэтому SO=kOA
и SO\perp OA
.
Высота OH
треугольника OPQ
соответствует высоте AD
треугольника ABC
, поэтому MD=OH=kAD
. Следовательно, прямоугольные треугольники AOS
и ADM
подобны, поэтому \angle OAS=\angle DAM
.
Обозначим \angle ACB=\alpha
. Тогда \angle CAD=90^{\circ}-\alpha
. С другой стороны, центральный угол AOB
вдвое больше вписанного угла ACB
, т. е. \angle AOB=2\alpha
. Из равнобедренного треугольника AOB
находим, что
\angle OAB=90^{\circ}-\frac{1}{2}\angle AOB=90^{\circ}-\alpha=\angle CAD.
Следовательно,
\angle BAS=\angle OAB+\angle OAS=\angle CAD+\angle DAM=\angle CAM.
Аналогично для AB\lt AC
.
Автор: Прокопенко Д. В.
Источник: Всероссийская олимпиада школьников. — 2009-10, XXXVI, заключительный этап, 10 класс
Источник: Журнал «Квант». — 2010, № 5, с. 50
