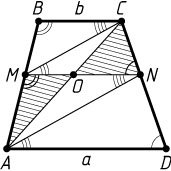
6623. Дана трапеция ABCD
с основаниями AD=a
и BC=b
. Точки M
и N
лежат на сторонах AB
и CD
соответственно, причём отрезок MN
параллелен основаниям трапеции. Диагональ AC
пересекает этот отрезок в точке O
. Найдите MN
, если известно, что площади треугольников AMO
и CNO
равны.
Ответ. \sqrt{ab}
.
Решение. Диагонали AC
и MN
четырёхугольника AMCN
пересекаются в точке O
и при этом треугольники AMO
и CNO
равновелики, значит, MC\parallel AN
(из равенства площадей треугольников AMN
и ACN
следует равенство их высот, опущенных из вершин M
и C
).
Треугольники MCN
и AND
подобны, поэтому \frac{MC}{AN}=\frac{MN}{AD}
. Треугольники MBC
и AMN
также подобны, поэтому \frac{MC}{AN}=\frac{BC}{MN}
. Следовательно, \frac{MN}{AD}=\frac{BC}{MN}
. Отсюда находим, что MN^{2}=AD\cdot BC=ab
.
Автор: Волчкевич М. А.
Источник: Московская математическая олимпиада. — 2010, LXXIII, 10 класс
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 4.49, с. 41
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 4.49.2, с. 42
