6626. В треугольнике ABC
точка I
— центр вписанной окружности. Точки M
и N
— середины сторон BC
и AC
соответственно. Известно, что угол AIN
прямой. Докажите, что угол BIM
— также прямой.
Решение. Центр окружности, вписанной в треугольник, есть точка пересечения его биссектрис, поэтому луч AI
— биссектриса угла BAC
.
Обозначим \angle IAN=\angle IAB=\alpha
. Поскольку MN
— средняя линия треугольника ABC
,
\angle ANM=180^{\circ}-\angle NAB=180^{\circ}-2\alpha,
а так как \angle AIN=90^{\circ}
, то
\angle ANI=90^{\circ}-\angle IAN=90^{\circ}-\alpha=\frac{1}{2}\angle ANM,
т. е. луч NI
— биссектриса угла ANM
. Следовательно, точка I
равноудалена от прямых AB
, AC
, BC
и MN
, значит, I
— центр окружности, вписанной в четырёхугольник ANMB
. Тогда MI
— биссектриса угла BMN
, а так как BI
— биссектриса угла ABM
, то \angle BIM=90^{\circ}
(как угол между биссектрисами внутренних односторонних углов при параллельных прямых и секущей). Что и требовалось доказать.
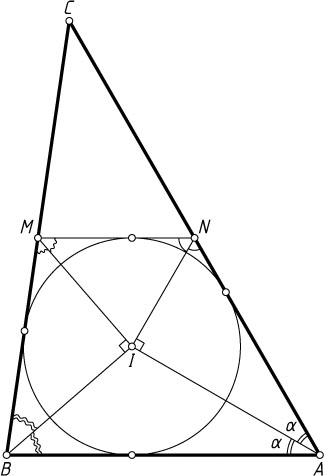
Примечание. См. статью А.Заславского «Приключения одной задачи», Квант, 2017, N12, с.19-21.
Автор: Заславский А. А.
Источник: Московская математическая олимпиада. — 2010, LXXIII, 8 класс
Источник: Журнал «Квант». — 2017, № 12, с. 20
