6655. В треугольнике ABC
известно, что \angle B=2\angle C
. Точки P
и Q
на серединном перпендикуляре к стороне CB
таковы, что \angle CAP=\angle PAQ=\angle QAB=\frac{1}{3}\angle A
. Докажите, что Q
— центр описанной окружности треугольника CPB
.
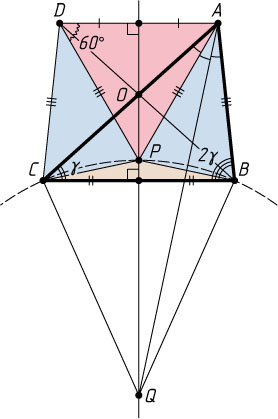
Решение. Обозначим \angle ACB=\gamma
. Тогда \angle ABC=2\gamma
. Пусть точка D
симметрична A
относительно серединного перпендикуляра к стороне BC
. Тогда ABCD
— равнобокая трапеция. Её диагонали AC
и BD
пересекаются в точке O
, лежащей на серединном перпендикуляре к BC
, значит, OB=OC
и
\angle OBC=\angle OCB=\gamma=\frac{1}{2}\angle ABC.
Поэтому диагональ BD
— биссектриса угла ABC
, \angle ADC=\angle CBD=\angle ABD
, треугольник ABD
— равнобедренный. Значит, CD=AB=AD
. Далее
\angle DAP=\angle CAD+\frac{1}{3}\angle CAP=\gamma+\frac{1}{3}(180^{\circ}-3\gamma)=60^{\circ}.
Поэтому треугольник ADP
— равносторонний и AP=AD=AB
. Поскольку AQ
— биссектриса угла PAB
равнобедренного треугольника PAB
, прямая AQ
— серединный перпендикуляр к отрезку PB
, поэтому QP=QB=QC
. Следовательно, Q
— центр описанной окружности треугольника CPB
.
Автор: Кеян Д.
Источник: Олимпиада по геометрии им. И. Ф. Шарыгина. — 2011, VII, финальный тур, № 2, 9 класс
