6659. В треугольнике ABC
середины сторон AC
, BC
, вершина C
и точка пересечения медиан лежат на одной окружности. Докажите, что она касается окружности, проходящей через вершины A
, B
и ортоцентр треугольника ABC
.
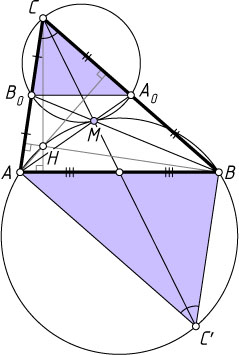
Решение. Пусть H
— ортоцентр треугольника ABC
, C'
— точка, симметричная C
относительно середины AB
. Поскольку
\angle AHB=180^{\circ}-\angle ACB=180^{\circ}-\angle AC'B,
точки A
, B
, C'
и H
лежат на одной окружности. С другой стороны, если A_{0}
и B_{0}
— середины сторон BC
и AC
соответственно, то треугольник A_{0}B_{0}C
гомотетичен треугольнику ABC'
относительно точки пересечения медиан M
треугольника ABC
с коэффициентом -\frac{1}{2}
. Следовательно, описанные окружности этих треугольников касаются в точке M
.
Автор: Рожкова М. Н.
Источник: Олимпиада по геометрии им. И. Ф. Шарыгина. — 2011, VII, финальный тур, № 1, 10 класс
