6665. В прямоугольном треугольнике ABC
(\angle C=90^{\circ}
) биссектрисы AA_{1}
и BB_{1}
пересекаются в точке I
. Пусть O
— центр описанной окружности треугольника CA_{1}B_{1}
. Докажите, что OI\perp AB
.
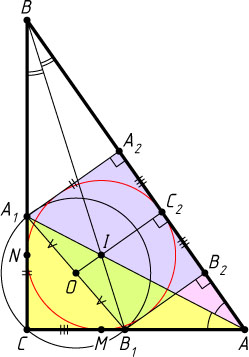
Решение. Первый способ. Поскольку I
— точка пересечения биссектрис треугольника ABC
, эта точка — центр его вписанной окружности (рис. 1). Пусть M
, N
и C_{2}
— точки касания этой окружности с катетами AC
, BC
и гипотенузой AB
соответственно, A_{2}
, B_{2}
— проекции точек соответственно A_{1}
и B_{1}
на AB
.
Точка A_{1}
лежит на биссектрисе угла BAC
, значит, она равноудалена от его сторон, поэтому CA_{1}=A_{1}A_{2}
и AA_{2}=AC
, а так как AM=AC_{2}
, то A_{2}C_{2}=CM
. Аналогично получаем, что B_{2}C_{2}=CN=CM
. Следовательно, A_{2}C_{2}=B_{2}C_{2}
, т. е. C_{2}
— середина отрезка A_{2}B_{2}
.
По теореме Фалеса прямая C_{2}I
пересекает отрезок A_{1}B_{1}
в его середине, а так как треугольник CA_{1}B_{1}
прямоугольный, то эта середина совпадает с центром O
его описанной окружности.
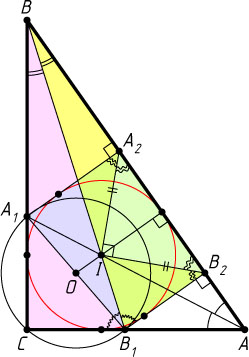
Второй способ (решение Арсения Райко, 179 школа, г. Москва). Обозначим через A_{2}
и B_{2}
основания перпендикуляров, опущенных из точек соответственно A_{1}
и B_{1}
на гипотенузу AB
(рис. 2). Из равенства прямоугольных треугольников BCB_{1}
и BB_{2}B_{1}
следует, что \angle BB_{1}C=\angle BB_{1}B_{2}
. Получаем, что для треугольника AB_{1}B_{2}
точка I
является центром вневписанной окружности. Следовательно, B_{2}I
— биссектриса прямого угла B_{1}B_{2}A_{2}
. Такими же рассуждениями показываем, что A_{2}I
является биссектрисой прямого угла A_{1}A_{2}B_{2}
. Таким образом, треугольник B_{2}IA_{2}
— равнобедренный и прямоугольный, т. е. точка I
лежит на серединном перпендикуляре к A_{2}B_{2}
. Точка O
— середина боковой стороны B_{1}A_{1}
прямоугольной трапеции B_{2}B_{2}A_{1}A_{2}
, значит, точка O
также лежит на серединном перпендикуляре A_{2}B_{2}
. Следовательно, OI\perp B_{2}A_{2}
.
