6667. Точки B_{1}
и B_{2}
лежат на луче AM
, а точки C_{1}
и C_{2}
— на луче AK
. Окружность с центром O
вписана в треугольники AB_{1}C_{1}
и AB_{2}C_{2}
. Докажите, что углы B_{1}OB_{2}
и C_{1}OC_{2}
равны.
Решение. Первый способ. Из условия следует, что если точка B_{1}
лежит между A
и B_{2}
, то точка C_{2}
лежит между A
и C_{1}
.
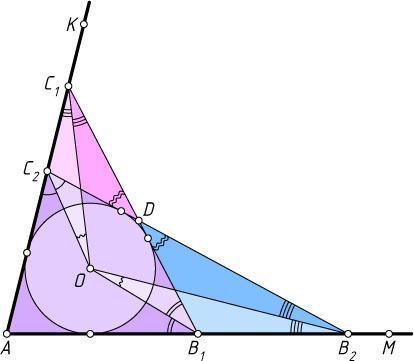
Пусть отрезки B_{1}C_{1}
и B_{2}C_{2}
пересекаются в точке D
. Тогда по теореме о внешнем угле треугольника
\angle B_{1}OB_{2}=\angle AB_{1}O-\angle AB_{2}O=\frac{1}{2}(\angle AB_{1}C_{1}-\angle AB_{2}C_{2})=\frac{1}{2}\angle B_{1}DB_{2}.
Аналогично
\angle C_{1}OC_{2}=\frac{1}{2}\angle C_{1}DC_{2}=\frac{1}{2}\angle B_{1}DB_{2}.
Следовательно, \angle B_{1}OB_{2}=\angle C_{1}OC_{2}
.
Второй способ. Из условия следует, что если точка B_{1}
лежит между A
и B_{2}
, то точка C_{2}
лежит между A
и C_{1}
.
Центр O
окружности, вписанной в треугольник AB_{1}C_{1}
, — точка пересечения биссектрис этого треугольника, поэтому
\angle B_{1}OC_{1}=90^{\circ}+\frac{1}{2}\angle MAN
(см. задачу 4770). Аналогично \angle B_{2}OC_{2}=90^{\circ}+\frac{1}{2}\angle MAN
. Значит, \angle B_{1}OC_{1}=\angle B_{2}OC_{2}
. Следовательно,
\angle B_{1}OB_{2}=\angle B_{1}OC_{1}-\angle B_{2}OC_{1}=\angle B_{2}OC_{2}-\angle B_{2}OC_{1}=\angle C_{1}OC_{2}.
Автор: Прокопенко Д. В.
Источник: Всероссийская олимпиада по геометрии. — 2009, 8-11 классы
Источник: Олимпиада по геометрии им. И. Ф. Шарыгина. — 2009, V, заочный тур, № 1, 8 класс
