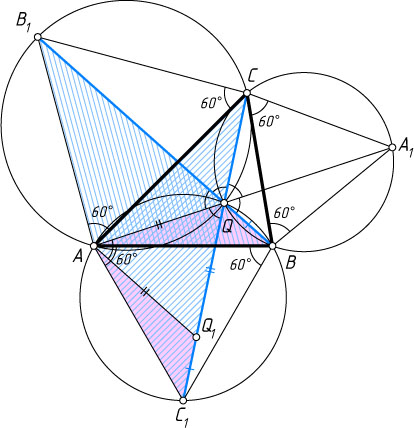
6703. Точка Торичелли. На сторонах треугольника ABC
построены вне треугольника равносторонние треугольники BCA_{1}
, CAB_{1}
, ABC_{1}
, и проведены отрезки AA_{1}
, BB_{1}
и CC_{1}
. Докажите, что
а) AA_{1}=BB_{1}=CC_{1}
;
б) прямые AA_{1}
, BB_{1}
и CC_{1}
пересекаются в одной точке;
в) если эта точка находится внутри треугольника ABC
, то сумма расстояний от неё до трёх вершин треугольника равна длине каждого из отрезков AA_{1}
, BB_{1}
, CC_{1}
.
Указание. Рассмотрите поворот на 60^{\circ}
вокруг точки A
, переводящий точку C_{1}
в B_{1}
.
Решение. При повороте на угол 60^{\circ}
вокруг вершины A
, переводящем точку C_{1}
в B
, точка C
переходит в точку B_{1}
. Следовательно, отрезок C_{1}C
переходит в отрезок BB_{1}
. Поэтому CC_{1}=BB_{1}
. Аналогично докажем, что AA_{1}=BB_{1}
. При этом угол между прямыми CC_{1}
и BB_{1}
равен 60^{\circ}
.
Пусть Q
— точка пересечения прямых BB_{1}
и CC_{1}
. Отрезок C_{1}B
виден из точек A
и Q
под углом 60^{\circ}
. Поэтому точка Q
лежит на описанной окружности треугольника ABC_{1}
. Аналогично докажем, что точка Q
лежит на описанной окружности треугольника CAB_{1}
. Поскольку
\angle BQC+\angle BA_{1}C=120^{\circ}+60^{\circ}=180^{\circ},
то точка Q
лежит и на описанной окружности треугольника BCA_{1}
. Тогда
\angle AQA_{1}=\angle AQB+\angle BQA_{1}=\angle AQB+\angle BCA_{1}=120^{\circ}+60^{\circ}=180^{\circ}.
Следовательно, прямая AA_{1}
проходит через точку Q
.
Рассмотрим теперь образ Q_{1}
точки Q
, лежащей внутри треугольника ABC
, при повороте на 60^{\circ}
относительно точки A
, переводящем B
в C_{1}
. При этом повороте треугольник AQB
переходит в треугольник AQ_{1}C_{1}
, а так как треугольник QAQ_{1}
равносторонний, то QQ_{1}=AQ
. Поэтому
C_{1}Q=C_{1}Q_{1}+Q_{1}Q=BQ+AQ.
Следовательно, C_{1}C=C_{1}Q+QC=BQ+AQ+CQ
. Аналогично для отрезков AA_{1}
и BB_{1}
.
Примечание. См. также статью Л.Радзивиловского «Ещё раз о точке Торричелли», Квант, 2014, N3, с.38-42.
Источник: Болтянский В. Г., Яглом И. М. Преобразования. Векторы. — М.: Просвещение, 1964. — № 222, с. 95
Источник: Адамар Ж. Элементарная геометрия. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1948. — № 105, с. 105
Источник: Пржевальский Е. Собрание геометрических теорем и задач. — М.: Типография Г. Лисснера и Д. Собко, 1909. — № 162, с. 46
Источник: Факультативный курс по математике: Учебное пособие для 7—9 кл. средней школы / Сост. И. Л. Никольская. — М.: Просвещение, 1991. — с. 98-99
Источник: Куланин Е. Д., Федин С. Н. Геометрия треугольника в задачах: Экспериментальное учебное пособие для 8—10 кл. школ физико-математического направления. — М.: НИИ школ, 1990. — № 40, с. 9
