6714. Пусть M
и N
— середины сторон CD
и DE
правильного шестиугольника ABCDEF
. Найдите угол между прямыми AM
и BN
.
Ответ. 60^{\circ}
.
Указание. Рассмотрите поворот на 60^{\circ}
вокруг центра шестиугольника.
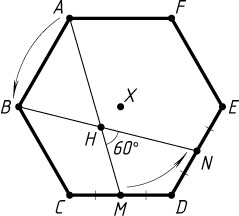
Решение. При повороте на 60^{\circ}
вокруг центра X
правильного шестиугольника ABCDEF
, переводящем вершину A
в вершину B
, вершина C
переходит в вершину D
, а вершина D
— в вершину E
. Поэтому середина M
отрезка CD
переходит в середину N
отрезка ED
, а прямая AM
— в прямую BN
. Следовательно, искомый угол равен 60^{\circ}
.
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 2. — М.: Наука, 1991. — № 18.16(а), с. 70
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 18.17(а), с. 375
