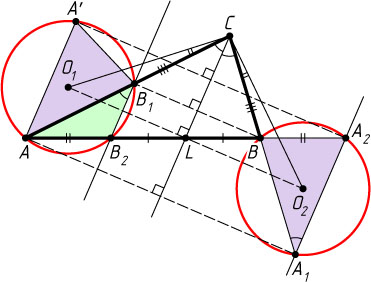
6720. В треугольнике ABC
провели биссектрису CL
. Точки A_{1}
и B_{1}
симметричны точкам A
и B
относительно прямой CL
, A_{2}
и B_{2}
симметричны точкам A
и B
относительно точки L
. Пусть O_{1}
и O_{2}
— центры окружностей, описанных около треугольников AB_{1}B_{2}
и BA_{1}A_{2}
. Докажите, что углы O_{1}CA
и O_{2}CB
равны.
Решение. Будем считать, что CA\gt BA
.
Из симметрии следует, что CB_{1}=CB
, а из свойства биссектрисы треугольника — \frac{CB}{CA}=\frac{BL}{LA}
. Значит,
\frac{CB_{1}}{CA}=\frac{CB}{CA}=\frac{BL}{LA}=\frac{B_{2}L}{AL}.
Следовательно, B_{1}B_{2}\parallel CL
. Аналогично A_{1}A_{2}\parallel CL
. Тогда
\angle AB_{1}B_{2}=\angle BA_{1}A_{2}=\frac{1}{2}\angle C.
При симметрии относительно прямой CL
точки B
и A_{1}
перейдут в B_{1}
и A
соответственно, а точка A_{2}
— в некоторую точку A'
. При этом треугольники AB_{1}A'
и A_{1}BA_{2}
равны, так как они симметричны относительно прямой CL
. Тогда
\angle A'AB_{2}=\angle A'AB_{1}+\angle B_{1}AB_{2}=\angle A_{2}A_{1}B+\angle CAB=
=\angle LCB+\angle CAB=\frac{1}{2}\angle C+\angle A,
\angle A'B_{1}B_{2}=\angle A'B_{1}A+\angle AB_{1}B_{2}=\angle A_{2}BA_{1}+\angle ACL=
=\angle ABC+\angle ACL=\angle B+\frac{1}{2}\angle C.
Значит,
\angle A'AB_{2}+\angle A'B_{1}B_{2}=\angle A+\angle B+2\cdot\frac{1}{2}\angle C=180^{\circ},
поэтому четырёхугольник AA'B_{1}B_{2}
вписанный, и точка A'
лежит на описанной окружности треугольника AB_{1}B_{2}
, которая симметрична описанной окружности треугольника A_{1}BA_{2}
. Тогда центры O_{1}
и O_{2}
этих окружностей симметричны относительно прямой CL
. Следовательно, углы O_{1}CA
и O_{2}CB
равны, так как они также симметричны относительно прямой CL
.
Автор: Прокопенко Д. В.
Источник: Олимпиада по геометрии им. И. Ф. Шарыгина. — 2009, V, заочный тур, № 12, 9-10 классы
Источник: Всероссийская олимпиада по геометрии. — 2009, 9-11 классы
