6726. Пусть AH_{a}
и BH_{b}
— высоты треугольника ABC
, P
и Q
— проекции точки H_{a}
на стороны AB
и AC
. Докажите, что прямая PQ
делит отрезок H_{a}H_{b}
пополам.
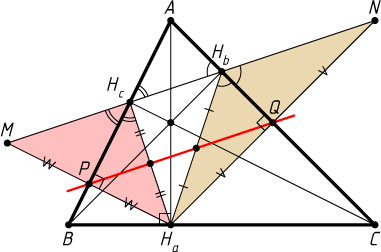
Решение. Пусть CH_{c}
— третья высота треугольника. Тогда
\angle H_{a}H_{c}B=\angle H_{b}H_{c}A=\angle C,
(см. задачу 141).
Пусть M
— точка пересечения прямых H_{b}H_{c}
и H_{a}P
. Поскольку
\angle MH_{c}P=\angle H_{b}H_{c}A=\angle H_{a}H_{c}P,
то H_{c}P
— высота и биссектриса треугольника H_{a}H_{c}M
. Значит, этот треугольник равнобедренный, и P
— середина H_{a}M
. Аналогично докажем, что точка Q
— середина отрезка H_{a}N
, где N
— точка пересечения прямых H_{b}H_{c}
и H_{a}Q
. Тогда PQ
— средняя линия треугольника MH_{a}N
. Следовательно, по теореме Фалеса отрезок H_{a}H_{b}
делится прямой PQ
пополам.
Автор: Акопян А. В.
Автор: Савенков К. С.
Источник: Олимпиада по геометрии им. И. Ф. Шарыгина. — 2009, V, финальный тур, № 3, 8 класс
Источник: Всероссийская олимпиада по геометрии. — 2009, 8 класс
