6738. В треугольник ABC
вписан ромб CKLN
так, что точка L
лежит на стороне AB
, точка N
— на стороне AC
, точка K
— на стороне BC
. Пусть O_{1}
, O_{2}
и O
— центры описанных окружностей треугольников ACL
, BCL
и ABC
соответственно. Пусть P
— точка пересечения описанных окружностей треугольников ANL
и BKL
, отличная от L
. Докажите, что точки O_{1}
, O_{2}
, O
и P
лежат на одной окружности.
Решение. Обозначим \angle ACB=\gamma
. Диагональ CL
ромба — биссектриса угла ACB
, а прямые LN
и LK
параллельны сторонам BC
и AC
. Кроме того, AO_{1}L
— центральный угол описанной окружности треугольника ACL
, а ACL
— вписанный, поэтому
\angle AO_{1}L=2\angle ACL=\angle ACB=\angle ANL,
т. е. точка O_{1}
лежит на описанной окружности треугольника ANL
. Вписанные в эту окружность углы APL
и AO_{1}L
равны, так как они опираются на одну и ту же дугу. Вписанные углы APO_{1}
и ALO_{1}
также равны, а треугольник AO_{1}L
равнобедренный, поэтому
\angle O_{1}PL=\angle APL+\angle O_{1}PA=\angle ANL+\angle O_{1}LA=
=\gamma+\left(90^{\circ}-\frac{\gamma}{2}\right)=90^{\circ}+\frac{\gamma}{2}.
Аналогично \angle O_{2}PL=90^{\circ}+\frac{\gamma}{2}
. Значит,
\angle O_{1}PO_{2}=360^{\circ}-2\left(90^{\circ}-\frac{\gamma}{2}\right)=180^{\circ}=\gamma,
но угол O_{1}OO_{2}
также равен 180^{\circ}-\gamma
, потому что прямые OO_{1}
и OO_{2}
являются серединными перпендикулярами к сторонам AC
и BC
. Из точек P
и O
отрезок O_{1}O_{2}
виден под одним и тем же углом, следовательно, точки O_{1}
, O_{2}
, O
и P
лежат на одной окружности. Что и требовалось доказать.
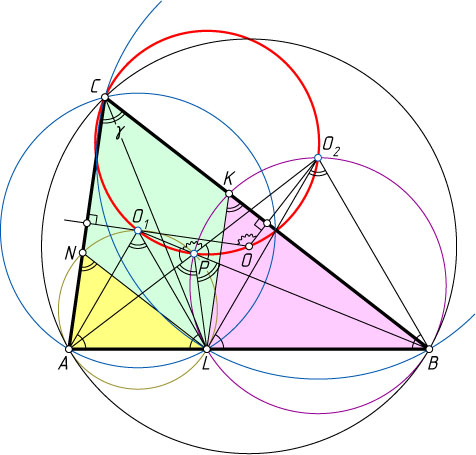
Автор: Прокопенко Д. В.
Источник: Олимпиада по геометрии им. И. Ф. Шарыгина. — 2009, V, финальный тур, № 5, 10 класс
Источник: Всероссийская олимпиада по геометрии. — 2009, 10 класс
