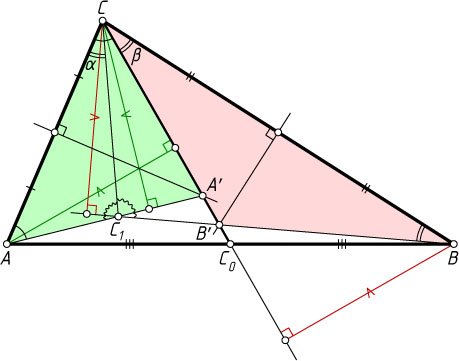
6745. Пусть CC_{0}
— медиана треугольника ABC
, серединные перпендикуляры к AC
и BC
пересекают CC_{0}
в точках A'
и B'
, прямые AA'
и BB'
пересекаются в точке C_{1}
. Докажите, что \angle C_{1}CA=\angle C_{0}CB
.
Решение. Треугольники CAA'
, и CBB'
— равнобедренные, поэтому
\angle CAA'=\angle C_{0}CA,~\angle CBB'=\angle C_{0}CB.
Следовательно, расстояния от точки C
до прямых AC_{1}
и BC_{1}
равны соответственно расстояниям от A
и B
до прямой CC_{0}
(как высоты равнобедренных треугольников, опущенные на боковые стороны). Но CC_{0}
— медиана, так что эти расстояния равны. Таким образом, точка C
равноудалена от прямых C_{1}A
и C_{1}B
, поэтому \angle CC_{1}A=\angle CC_{1}B
. Отсюда получаем, что
\angle C_{1}CA-\angle C_{1}CB=\angle C_{1}BC-\angle C_{1}AC=\angle C_{0}CB-\angle C_{0}CA,
значит,
\angle C_{1}CA+\angle C_{0}CA=\angle C_{1}CB+\angle C_{0}CB.
Обозначим \angle C_{1}CA=\alpha
, \angle C_{0}CB=\beta
. Тогда последнее равенство имеет вид
2\alpha+\angle C_{1}CC_{0}=2\beta+\angle C_{1}CC_{0}.
Следовательно, \alpha=\beta
. Что и требовалось доказать.
Автор: Нилов Ф. К.
Автор: Заславский А. А.
Источник: Олимпиада по геометрии им. И. Ф. Шарыгина. — 2008, IV, финальный тур, № 4, 8 класс
