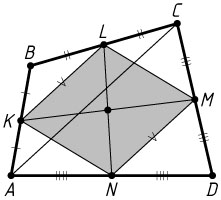
6761. Дан четырёхугольник ABCD
.
а) Докажите, что отрезки LN
и KM
, соединяющие середины его противоположных сторон, делят друг друга пополам.
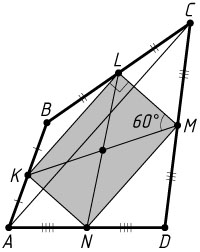
б) Найдите площадь четырёхугольника ABCD
, если LM=3\sqrt{3}
, KM=6\sqrt{3}
, \angle KML=60^{\circ}
.
Ответ. 54\sqrt{3}
.
Решение. а) Пусть K
, L
, M
и N
— середины сторон соответственно AB
, BC
, CD
и AD
четырёхугольника ABCD
. Тогда KL
и MN
— средние линии треугольников ABC
и ADC
. Значит, KL=\frac{1}{2}AC=MN
и KL\parallel AC\parallel MN
, поэтому KLMN
— параллелограмм. Его диагонали KM
и LN
делят друг друга пополам. Что и требовалось доказать.
б) Сторона LM
треугольника KLM
вдвое меньше стороны KM
, а угол между этими сторонами равен 60^{\circ}
, значит, треугольник KLM
прямоугольный с прямым углом при вершине L
. Тогда
KL=LM\tg60^{\circ}=3\sqrt{3}\cdot\sqrt{3}=9.
Четырёхугольник KLMN
— прямоугольник, поэтому
S_{KLMN}=KL\cdot LM=9\cdot3\sqrt{3}=27\sqrt{3}.
Пусть искомая площадь четырёхугольника ABCD
равна S
. Поскольку KL
— средняя линия треугольника ABC
, то S_{\triangle KBL}=\frac{1}{4}S_{\triangle ABC}
. Аналогично S_{\triangle MDN}=\frac{1}{4}S_{\triangle ADC}
. Значит,
S_{\triangle KBL}+S_{\triangle MDN}=\frac{1}{4}S_{\triangle ABC}+\frac{1}{4}S_{\triangle ADC}=\frac{1}{4}(S_{\triangle ABC}+S_{\triangle ADC})=\frac{1}{4}S.
Аналогично S_{\triangle CML}+S_{\triangle AKN}=\frac{1}{4}S
. Поэтому
S_{KLMN}=S-\frac{1}{4}S-\frac{1}{4}S=\frac{1}{2}S.
Следовательно,
S=2S_{KLMN}=2\cdot27\sqrt{3}=54\sqrt{3}.
Источник: Диагностические и тренировочные задачи ЕГЭ. — 2014
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 3.26.1, с. 29

