6778. На гипотенузе KL
равнобедренного прямоугольного треугольника KLM
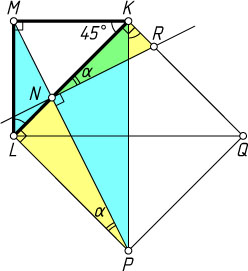
вне треугольника построен квадрат KLPQ
. Прямая MP
пересекает гипотенузу KL
в точке N
.
а) Докажите, что KN:NL=2:1
.
б) Прямая, проходящая через точку N
перпендикулярно MP
, пересекает отрезок KQ
в точке R
. Найдите KR
, если KQ=1
.
Ответ. \frac{2}{9}
.
Решение. а) Поскольку \angle QKP=45^{\circ}=\angle KLM
, прямые KP
и ML
параллельны, значит, треугольник KNP
подобен треугольнику LNM
, причём коэффициент подобия равен
\frac{KP}{LM}=\frac{KL\sqrt{2}}{\frac{KP}{\sqrt{2}}}=2.
Следовательно, \frac{KN}{NL}=\frac{KP}{LM}=2
. Что и требовалось доказать.
б) Заметим, что углы KNR
и LPN
равны как углы с соответственно перпендикулярными сторонами. По теореме косинусов
MN=\sqrt{ML^{2}+LN^{2}-2ML\cdot LN\cos45^{\circ}}=\sqrt{\frac{1}{2}+\frac{1}{9}-2\cdot\frac{1}{\sqrt{2}}\cdot\frac{1}{3}\cdot\frac{1}{\sqrt{2}}}=
=\sqrt{\frac{1}{2}+\frac{1}{9}-\frac{1}{3}}=\frac{\sqrt{5}}{3\sqrt{2}}.
Тогда, так как треугольники KNP
и LNM
подобны с коэффициентом 2, то
NP=2MN=\frac{2\sqrt{5}}{3\sqrt{2}}=\frac{\sqrt{10}}{3}.
Обозначим \angle KNR=\angle LPN=\alpha
. Из прямоугольного треугольника LPN
находим, что
\sin\alpha=\frac{NL}{NP}=\frac{\frac{1}{3}}{\frac{\sqrt{10}}{3}}=\frac{1}{\sqrt{10}}.
Тогда
\cos\alpha=\frac{3}{\sqrt{10}},~\tg\alpha=\frac{1}{3}.
Следовательно,
KR=KN\tg\angle KNR=\frac{2}{3}\cdot\tg\alpha=\frac{2}{3}\cdot\frac{1}{3}=\frac{2}{9}.
Источник: Диагностические и тренировочные задачи ЕГЭ. — 2015
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 1, с. 173
