6779. К окружности, вписанной в квадрат ABCD
, проведена касательная, пересекающая стороны AB
и AD
в точках M
и N
соответственно.
а) Докажите, что периметр треугольника AMN
равен стороне квадрата.
б) Прямая MN
пересекает прямую CD
в точке P
. В каком отношении делит сторону BC
прямая, проходящая через точку P
и центр окружности, если AM:MB=1:3
?
Ответ. 1:3
.
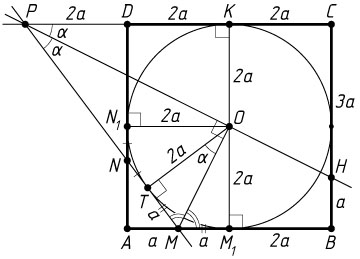
Решение. а) Пусть окружность, вписанная в квадрат, касается его стороны AB
в точке M_{1}
, стороны AD
— в точке N_{1}
, а прямой MN
— в точке T
. Тогда
MM_{1}=MT,~NN_{1}=NT,~AM+MN+AN=AM+MT+NT+AN=
=(AM+MM_{1})+(NN_{1}+AN)=\frac{1}{2}AB+\frac{1}{2}AD=AB.
б) Положим AB=4a
. Тогда радиус окружности равен 2a
, AM=\frac{1}{4}AB=a
.
Пусть O
— центр окружности. Тогда
MT=MM_{1}=AM_{1}-AM=2a-a=a.
Треугольник POM
прямоугольный, поскольку \angle MOP=90^{\circ}
как угол между биссектрисами внутренних односторонних углов при параллельных прямых AB
, PC
и секущей MP
. Пусть K
— точка касания окружности со стороной CD
, H
— точка пересечения прямой PO
со стороной BC
. Обозначим \angle MOT=\alpha
. Тогда
\angle OPK=\angle OPM=\angle MOT=\alpha,~\tg\alpha=\frac{MT}{OT}=\frac{a}{2a}=\frac{1}{2},
PK=OK\ctg\alpha=2a\cdot2=4a,~CP=PK+KC=4a+2a=6a,
значит,
CH=CP\tg\alpha=6a\cdot\frac{1}{2}=3a,~BH=BC-CH=4a-3a=a.
Следовательно,
\frac{BH}{CH}=\frac{a}{3a}=\frac{1}{3}.
Источник: ЕГЭ. — 2015
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 11.52.1, с. 120
