6786. На основании AC
равнобедренного треугольника ABC
взяли произвольную точку X
, а на боковых сторонах — точки P
и Q
так, что XPBQ
— параллелограмм. Докажите, что точка Y
, симметричная точке X
относительно PQ
, лежит на описанной окружности треугольника ABC
.
Решение. Пусть точка P
лежит на стороне AB
, а точка Q
— на стороне BC
.
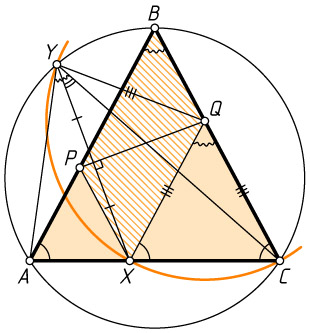
Первый способ. Поскольку PBQX
— параллелограмм, BP=QX
и \angle BAC=\angle QXC
(рис. 1). Треугольник ABC
равнобедренный, поэтому \angle BAC=\angle BCA
. Отсюда \angle QXC=\angle BCA
и QX=QC
. Из того, что точки X
и Y
симметричны относительно PQ
, также следует равенство QX=QY
. Значит, точки X
, C
и Y
лежат на окружности с центром в точке Q
, поэтому
\angle CYX=\frac{1}{2}\angle CQX=\frac{1}{2}\angle B.
Аналогично, \angle AYX=\frac{1}{2}\angle B
. Отсюда \angle CYA=\angle B
и, следовательно, точки A
, B
, C
и Y
лежат на одной окружности.
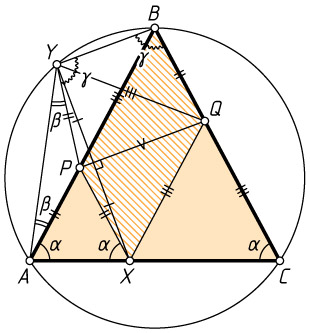
Второй способ. Треугольник ABC
равнобедренный, а прямые PX
и BQ
параллельны, поэтому
\angle BAC=\angle BCA=\angle PXA=\alpha.
Значит, треугольник PXA
также равнобедренный, PA=PX=PY
(рис. 2). Следовательно, треугольник APY
также равнобедренный, поэтому
\angle YAP=\angle AYP=\beta.
Треугольники YPQ
и BQP
равны по трём сторонам. Значит, точки B
и Y
расположены по одну сторону от прямой PQ
на одинаковом расстоянии от неё, поэтому прямая BY
параллельна прямой PQ
. Следовательно, BQPY
— равнобедренная трапеция, а углы при её основании BY
равны: \angle QBY=\angle PYB=\gamma
.
Наконец, в четырёхугольнике AYBC
имеем:
\angle ACB+\angle AYB=\alpha+\beta+\gamma=\angle CAY+\angle CBY,
т. е. суммы противоположных углов равны. Таким образом, этот четырёхугольник — вписанный.
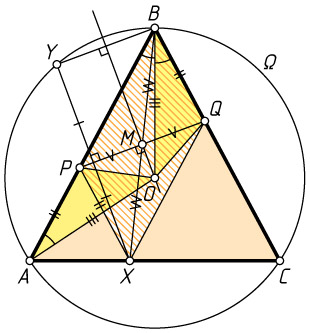
Третий способ. Пусть O
— центр описанной окружности \Omega
треугольника ABC
(рис. 3), M
— центр параллелограмма BPXQ
. Треугольники AOB
и ABC
равнобедренные, поэтому
\angle BAO=\angle ABO=\angle OBQ.
Значит, треугольники APO
и BQO
равны по двум сторонам и углу между ними. Следовательно, OP=OQ
, т. е. OM
— серединный перпендикуляр к отрезку PQ
.
Заметим, что точку Y
можно получить в два этапа: сначала отразить X
относительно точки M
, а затем отразить полученную точку B
относительно прямой OM
, перпендикулярной PQ
. Теперь очевидно, что Y
лежит на окружности \Omega
.
