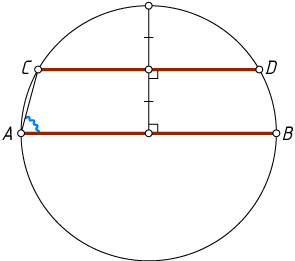
6810. В окружности провели диаметр AB
и параллельную ему хорду CD
так, что расстояние между ними равно половине радиуса этой окружности (см. рисунок). Найдите угол CAB
.
Ответ. 75^{\circ}
.
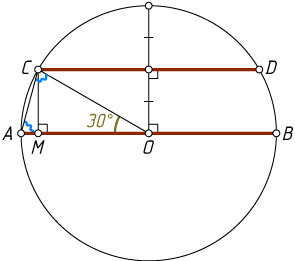
Решение. Рассмотрим треугольник AOC
, где O
— центр окружности. Этот треугольник равнобедренный, так как OC
и OA
— радиусы. Значит, по свойству равнобедренного треугольника, углы A
и C
равны.
Проведём перпендикуляр CM
к стороне AO
и рассмотрим прямоугольный треугольник OMC
. По условию задачи, катет CM
— половина гипотенузы OC
. Значит, \angle COM=30^{\circ}
. Тогда по теореме о сумме углов треугольника получаем, что угол
\angle CAB=\angle CAO=75^{\circ}.
Источник: Всероссийская олимпиада школьников. — 2014-2015, XLI, школьный этап, 9 класс

