6812. В неравнобедренном треугольнике ABC
провели биссектрисы угла ABC
и угла, смежного с ним. Они пересекли прямую AC
в точках B_{1}
и B_{2}
соответственно. Из точек B_{1}
и B_{2}
провели касательные к окружности, вписанной в треугольник ABC
, отличные от прямой AC
. Они касаются этой окружности в точках K_{1}
и K_{2}
соответственно. Докажите, что точки B
, K_{1}
и K_{2}
лежат на одной прямой.
Решение. Обозначим через I
центр окружности \omega
, вписанной в треугольник ABC
. Пусть D
— точка касания \omega
со стороной AC
. Прямая BB_{1}
проходит через центр \omega
, поэтому точки D
и K_{1}
симметричны относительно прямой BB_{1}
, т. е. BB_{1}
— биссектриса угла K_{1}BD
. Докажем, что BI
также является биссектрисой угла K_{2}BD
; отсюда будет следовать требуемое.
Рассмотрим окружность, построенную на B_{2}I
как на диаметре. Внутренняя и внешняя биссектрисы угла треугольника перпендикулярны, а B_{2}K_{2}
и B_{2}D
касаются \omega
, поэтому
\angle B_{2}BI=\angle B_{2}K_{2}I=\angle B_{2}DI=90^{\circ}.
Значит, точки I
, B
, D
и K_{2}
лежат на окружности \Omega
с диаметром B_{2}I
. Радиусы ID
и IK_{2}
окружности \omega
равны, поэтому равны и стягиваемые ими дуги окружности \Omega
. Следовательно, \angle IBD=\angle IBK_{2}
, т. е. BI
— биссектриса угла K_{2}BD
. Это нам и требовалось.
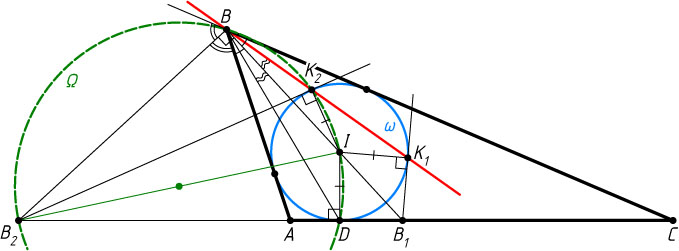
Автор: Емельянов Л. А.
Источник: Всероссийская олимпиада школьников. — 2014-2015, XLI, региональный этап, 9 класс
