6816. Дан остроугольный треугольник ABC
. Окружности с центрами A
и C
проходят через точку B
, вторично пересекаются в точке F
и пересекают описанную около треугольника ABC
окружность \omega
в точках D
и E
. Отрезок BF
пересекает окружность \omega
в точке O
. Докажите, что O
— центр описанной окружности треугольника DEF
.
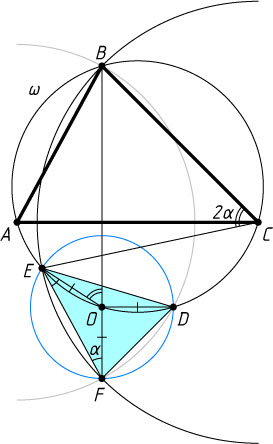
Решение. Докажем сначала, что OE=OF
. Для этого не нужна окружность с центром в точке A
. Рассмотрим чертёж без неё. Пусть в окружности с центром C
центральный угол BCE
равен 2\alpha
. Тогда вписанный угол EFB
равен \alpha
.
В окружности \omega
углы BCE
и BOE
вписанные и опираются на одну дугу, значит, \angle BOE=\angle BCE=2\alpha
. Угол BOE
— внешний угол треугольника EOF
. Следовательно,
\angle OEF=\angle BOE-\angle OFE=\alpha,
т. е. треугольник EOF
равнобедренный, OE=OF
.
Аналогично, рассмотрев окружность с центром A
, докажем, что OF=OD
. Следовательно, O
— центр описанной окружности треугольника DEF
.
