6817. Пусть AL
— биссектриса треугольника ABC
. Серединный перпендикуляр к отрезку AL
пересекает окружность, описанную около треугольника ABC
, в точках P
и Q
. Докажите, что окружность, описанная около треугольника PLQ
, касается стороны BC
.
Решение. Заметим, что треугольники PLQ
и PAQ
симметричны относительно прямой PQ
. Через точку A
проведём касательную XY
к окружности, на которой лежат точки A
, B
, C
, P
, Q
. Для решения задачи достаточно доказать, что прямые XY
и BC
симметричны относительно прямой PQ
, а так как точки A
и L
симметричны относительно прямой PQ
, остаётся установить равенство углов XAL
и BLA
.
Пусть точки X
и C
лежат по разные стороны от прямой AB
. Используя касание и теорему о внешнем угле треугольника, получим, что
\angle XAL=\angle XAB+\angle BAL=\angle ACB+\angle CAL=\angle ACL+\angle CAL=\angle BLA,
что и требовалось.
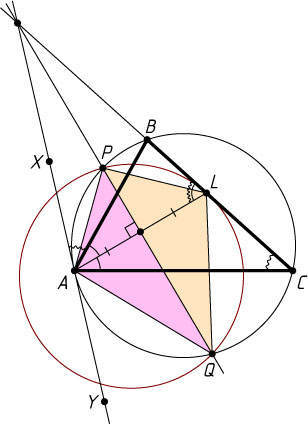
Автор: Берлов С. Л.
Источник: Всероссийская олимпиада школьников. — 2014-2015, XLI, региональный этап, 10 класс
